

Next: Concept of Strain
Up: No Title
Previous: Concept of Stress
Consider a small cube of sides
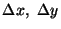 and
and 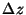 with its
centroid at point Q. Since different faces of the cube do not pass through
the same point, the state of stress on them will be different. We assume that
each component of stress is a continuously differentiable function of
with its
centroid at point Q. Since different faces of the cube do not pass through
the same point, the state of stress on them will be different. We assume that
each component of stress is a continuously differentiable function of
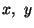 and z.
For a continuously differentiable function f of x,
and z.
For a continuously differentiable function f of x,
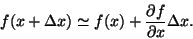 |
(3.1) |
The components of stress on the six faces of the cube are shown in Fig. 3.1

Let the gravitational force
g with components 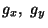 and gz act at every point of the cube;
g is measured as
force/mass. The equilibrium of forces in the x-direction gives
and gz act at every point of the cube;
g is measured as
force/mass. The equilibrium of forces in the x-direction gives
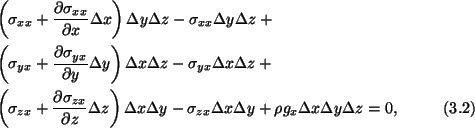
or
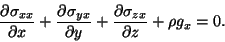 |
(3.3) |
Similarly
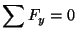 , and
, and
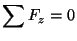 give
give
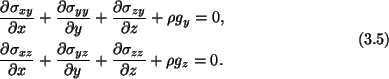
Here 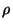 is the mass density per unit volume of the body.
Now take moments about the z-axis passing through the centroid of the cube.
is the mass density per unit volume of the body.
Now take moments about the z-axis passing through the centroid of the cube.
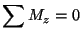 gives
gives
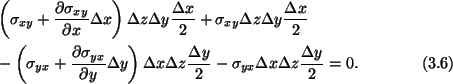
Divide by
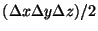 to obtain
to obtain
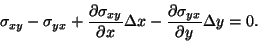 |
(3.7) |
Let
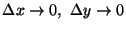 and
and
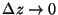 , and assume that
, and assume that
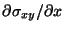 and
and
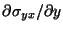 are bounded. Equation (3.7) reduces to
are bounded. Equation (3.7) reduces to
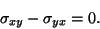 |
(3.8) |
Similarly

Thus the balance of moments implies the symmetry of the stress components.
Results: Equations of Equilibrium:
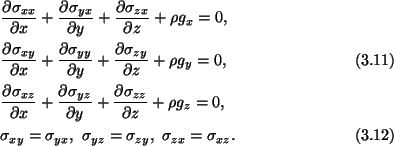
In condensed notation, we write
![\begin{displaymath}\{\sigma\}^T = [\sigma_{xx}\ \ \sigma_{yy}\ \ \sigma_{zz}\ \
\sigma_{yz}\ \ \sigma_{zx}\ \ \sigma_{xy}],\tag{3.13}
\end{displaymath}](img41.gif) |
(3.13) |
and in matrix notation
![\begin{displaymath}[{\mbox{\boldmath {$\sigma$ }}} ]= \left[\begin{array}{ccc}
\...
..._{zx} & \sigma_{zy} & \sigma_{zz}\end{array}\right].\tag{3.14}
\end{displaymath}](img42.gif) |
(3.14) |


Next: Concept of Strain
Up: No Title
Previous: Concept of Stress
Norma Guynn
1998-09-09
![]() and
and ![]() with its
centroid at point Q. Since different faces of the cube do not pass through
the same point, the state of stress on them will be different. We assume that
each component of stress is a continuously differentiable function of
with its
centroid at point Q. Since different faces of the cube do not pass through
the same point, the state of stress on them will be different. We assume that
each component of stress is a continuously differentiable function of
![]() and z.
For a continuously differentiable function f of x,
and z.
For a continuously differentiable function f of x,

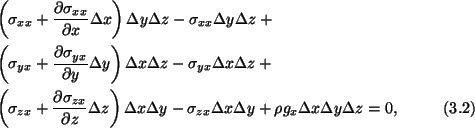
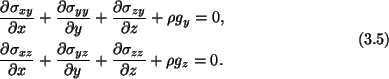
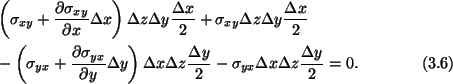
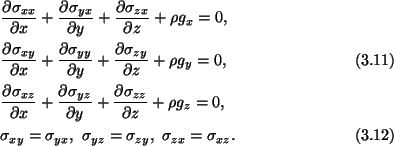
![\begin{displaymath}[{\mbox{\boldmath {$\sigma$ }}} ]= \left[\begin{array}{ccc}
\...
..._{zx} & \sigma_{zy} & \sigma_{zz}\end{array}\right].\tag{3.14}
\end{displaymath}](img42.gif)