Dislocation Emission in Fe
David C. Haeberle
Assignment 3
ESM 4984
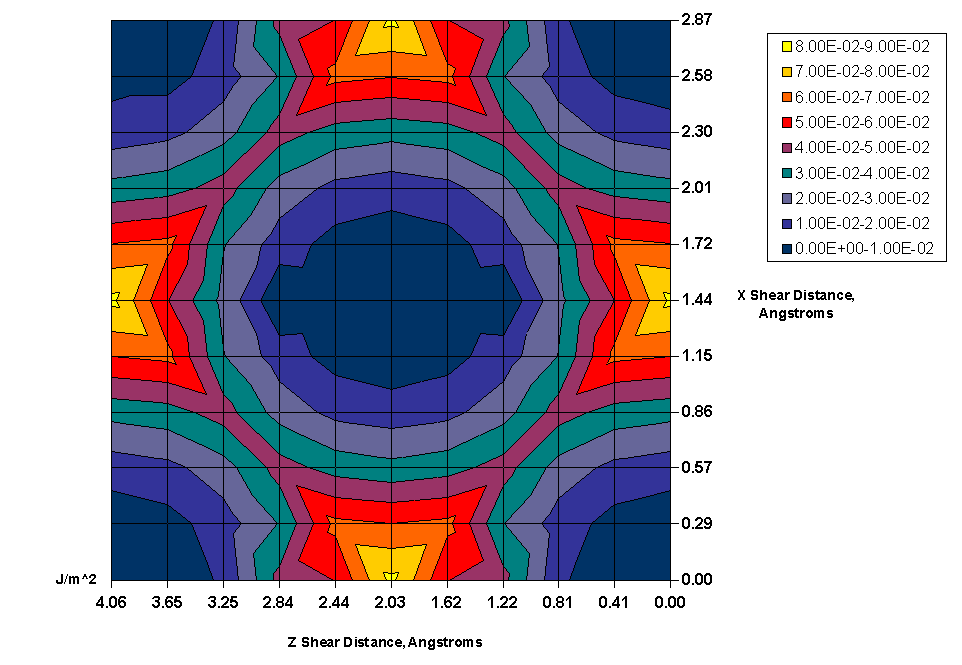
The blunting of sharp cracks is a very common occurrence in ductile metals and is a main reason for high fracture toughness in these materials. The blunting of the crack is due to the emission of dislocations at the crack tip. The emission of these dislocations is highly dependent on the orientation of the crystal structure at the crack tip because the dislocation follows the path of least resistance. The path of least resistance has three variables: (1) the crystal plane the dislocation travels, (2) the x shear distance, (3) z shear distance. The contour plot shown in Figure 1 represents the energy required to emit a dislocation in the x-z directions of the [110] plane of BCC iron (the slip plane for BCC metals).
Figure 1: [110] Energy Potentials for BCC Fe

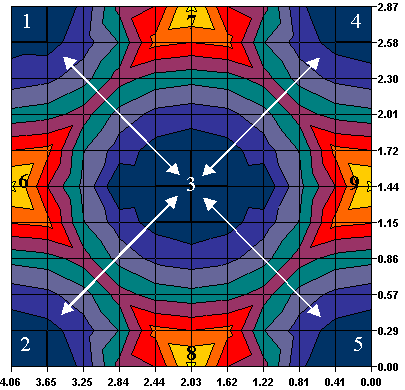
The [110] plane requires the lowest amount of energy to slip, therefore, dislocations always emit from the crack tip on this plane. From the figure, it is evident that even though this is the preferred plane, there are only certain directions the plane will travel. The atoms (represented by blue or low energy, in Figure 1) want to avoid being directly over top of atoms on another plane (represented by the orange and yellow regions in Figure 1). Figure 2 shows the direction the [110] plane would slip and show where the atoms are on a typical BCC cube. The blue atoms in the BCC structure in Figure 2 would slip in relation to the orange atoms in the directions shown on the contour plot.
Figure 2: Atomic Slip Directions in the [110] Place
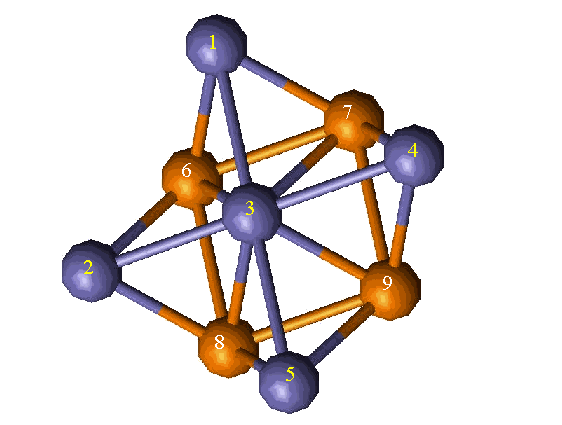
Current literature evaluates the energies associated with unstable stacking faults in various metallic alloys. These energies are similar to the worst case for the [110] plane of BCC Fe. The highest value simulated was at position 6 in Figure 2 where the stacking fault energy reached 0.483 J/m2 (not shown in the contour plot). This position is directly above another atom, and its energy is not shown on the contour plot because is much larger than all others calculated, making it difficult to plot. Most of the energies calculated, however, were in on the order of 10-2, much lower than the values in the literature.
Table 1: Calculated Surface Energies (J/m2)
|
X¯ Z® |
0 |
0.405879 |
0.811759 |
1.217638 |
1.623517 |
2.029396 |
2.435276 |
2.841155 |
3.247034 |
3.652914 |
4.058793 |
|
0 |
5.86E-14 |
2.77E-03 |
1.16E-02 |
4.31E-02 |
5.03E-02 |
8.26E-02 |
5.03E-02 |
4.31E-02 |
1.16E-02 |
2.77E-03 |
5.86E-14 |
|
0.287 |
3.52E-03 |
6.27E-03 |
1.50E-02 |
3.05E-02 |
6.29E-02 |
6.02E-02 |
6.29E-02 |
3.05E-02 |
1.50E-02 |
6.27E-03 |
3.52E-03 |
|
0.574 |
1.44E-02 |
1.71E-02 |
2.58E-02 |
4.44E-02 |
3.59E-02 |
3.32E-02 |
3.59E-02 |
4.44E-02 |
2.58E-02 |
1.71E-02 |
1.44E-02 |
|
0.861 |
3.32E-02 |
3.59E-02 |
4.44E-02 |
2.58E-02 |
1.71E-02 |
1.44E-02 |
1.71E-02 |
2.58E-02 |
4.44E-02 |
3.59E-02 |
3.32E-02 |
|
1.148 |
6.02E-02 |
6.29E-02 |
3.05E-02 |
1.50E-02 |
6.27E-03 |
3.52E-03 |
6.27E-03 |
1.50E-02 |
3.05E-02 |
6.29E-02 |
6.02E-02 |
|
1.435 |
8.26E-02 |
5.03E-02 |
2.71E-02 |
1.30E-03 |
2.77E-03 |
5.86E-14 |
2.77E-03 |
1.30E-03 |
2.71E-02 |
5.03E-02 |
8.26E-02 |
|
1.722 |
6.02E-02 |
6.29E-02 |
3.05E-02 |
1.50E-02 |
6.27E-03 |
3.52E-03 |
6.27E-03 |
1.50E-02 |
3.05E-02 |
6.29E-02 |
6.02E-02 |
|
2.009 |
3.32E-02 |
3.59E-02 |
4.44E-02 |
2.58E-02 |
1.71E-02 |
1.44E-02 |
1.71E-02 |
2.58E-02 |
4.44E-02 |
3.59E-02 |
3.32E-02 |
|
2.296 |
1.44E-02 |
1.71E-02 |
2.58E-02 |
4.44E-02 |
3.59E-02 |
3.32E-02 |
3.59E-02 |
4.44E-02 |
2.58E-02 |
1.71E-02 |
1.44E-02 |
|
2.583 |
3.52E-03 |
6.27E-03 |
1.50E-02 |
3.05E-02 |
6.29E-02 |
6.02E-02 |
6.29E-02 |
3.05E-02 |
1.50E-02 |
6.20E-03 |
6.27E-03 |
|
2.87 |
5.86E-14 |
2.77E-03 |
1.16E-02 |
4.31E-02 |
5.03E-02 |
8.26E-02 |
5.03E-02 |
4.31E-02 |
1.16E-02 |
2.77E-03 |
1.11E-11 |
Reference:
Farkas, D. et al. "Embedded atom calculations of unstable stacking fault energies and surface energies in intermetallics." Journal for Materials Research. Vol. 12, No. 1, Jan. 1997.