Concept of Stress

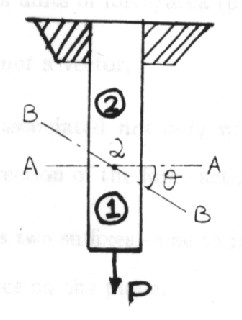
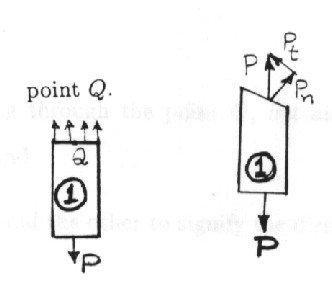
Consider a bar loaded by an axial force P as shown in Fig. 2.1.

  

Imagine that the bar is cut at plane AA passing through point Q; a free-body diagram of part $\bigcirc \!\!\!\! \scriptstyle{1}\$is shown in Fig. 2.2. Since part $\bigcirc \!\!\!\! \scriptstyle{1}\$ is in equilibrium, part $\bigcirc \!\!\!\! \scriptstyle{2}\$ of the bar must exert a force on part $\bigcirc \!\!\!\! \scriptstyle{1}\$ at the cut section, and the resultant of this force must equal P, be colinear with P and act in the opposite direction. Why? Otherwise, the bar will not be in equilibrium. The quantity

$$\sigma = \frac{\vert\mathbf{P}\vert}{\vert{\cal A}_{AA}\vert} = \frac{P}{{\cal A}_{AA}} \tag{2.1}$$ (2.1)

is called the average axial stress or the average normal stress at Q. Here ${\cal A}_{AA}$ is the area of cross-section of the bar at point Q; that is, area of the bar cut by the plane AA. Usually, the adjective `average' is dropped and $\sigma$ is referred to as the axial or the normal stress. The prefix axial or normal signifies that the resultant force on the plane AA passing through the point Q is acting along the axis of the bar or is along the normal to the section AA.

Now imagine the bar to be cut by the plane BB passing through the point Q. Again, for equilibrium, the resultant of forces exerted by part $\bigcirc \!\!\!\! \scriptstyle{2}\$ on part $\bigcirc \!\!\!\! \scriptstyle{1}\$at the cut section BB must be equal and opposite to P and be colinear with it. We can resolve P into two components: P_n along the normal to the section BB and P_tparallel to the section BB. The normal stress, $\sigma_{nn}$, at point Qon plane BB is defined by

$$\sigma_{nn} = \frac{\vert\mathbf{P}_n\vert}{\vert{\cal A}_{BB... ...cos\theta}{{\cal A}/\cos\theta} = \sigma\cos^2\theta \tag{2.2}$$ (2.2)

and

$$\sigma_{nt} = \frac{\vert\mathbf{P}_t\vert}{\vert{\cal A}_{BB... ...{\cal A}/\cos\theta} = \sigma \sin\theta \cos \theta \tag{2.3}$$ (2.3)

is the shear (or tangential) stress at Q on plane BB.

Note that the stress at any point Q

a)

has units of force/area (psi or Pa),

b)

is not a vector,

c)

is associated not only with a plane passing through the point Q, but also with the direction of the force acting on the plane, and

d)

has two suffixes - one to indicate the plane and the other to signify the direction of the force on the plane.

$\sigma$ in Eqn. (2.1) should have been denoted by $\sigma_{aa}$ to signify the axial direction of the force and the fact that the normal to the plane AA is along the axis of the bar. Note that the orientation of a plane in space is specified by the unit normal to the plane. The first suffix on ${\mbox{\boldmath {$\sigma$ }}}$ denotes the direction of the normal to the plane, and the second suffix indicates the direction of the force acting on the plane. We will see later that the suffixes/indices on ${\mbox{\boldmath {$\sigma$ }}}$ can be interchanged.

The aforestated simple exercise shows that at the same point Q, different normal and tangential stresses act on different planes passing through Q. Since there are infinitely many planes passing through the point Q, the following question arises. Through point Q, on how many planes do we need to find the normal and shear stresses in order to find the stress state on every plane through Q? Answer: Three mutually perpendicular planes. This result is known as Cauchy's Theorem, and we will not prove it in this course. Let these three mutually perpendicular planes be normal to $x,\ y$ and z-axes. The stress state on these three planes passing through a point is depicted in Fig. 2.3.

Recall that the first subscript on ${\mbox{\boldmath {$\sigma$ }}}$ stands for the normal to the surface on which ${\mbox{\boldmath {$\sigma$ }}}$ acts, and the second subscript for the direction of the force on the plane.

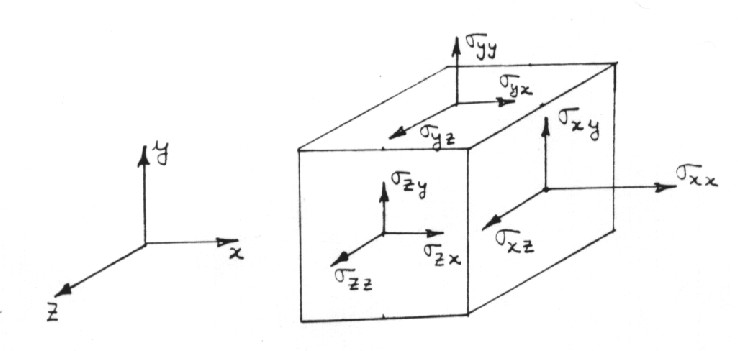
Recall the stress transformation equations you learned in the first course on Mechanics of Deformable Bodies. These equations express normal and shear stresses on a plane in terms of those acting on planes parallel to the co-ordinate axes. The same objective is accomplished by using Mohr's circle. One should keep in mind that all of these planes pass through the same point.

If the outward normal to a plane points in the positive x-direction, then it is called positive x-plane. Positive values of $\sigma_{xx}$ imply that the force $\sigma_{xx}\Delta y\Delta z$ acts in the positive x-direction, and positive values of $\sigma_{xy}$ imply that the force $\sigma_{xy}\Delta y\Delta z$ acts along the positive y-axis. Positive normal stresses are usually called tensile and negative normal stresses as compressive.