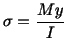An example of an ad-hoc approach.

Consider the problem of the bending of a beam usually studied in the first course on Mechanics of Deforms. This is generally based on the following assumptions:

i)

The beam is initially straight.

ii)

The cross-section is uniform.

iii)

The beam is made of a homogeneous and isotropic material which obeys Hooke's law.

iv)

Plane sections remain plane.

v)

The beam is subjected to a pure bending moment 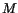$M$ applied at the ends.

Under these assumptions, one can derive the formula

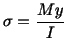$$\sigma = \frac{My}{I}$$ (1.3.1)

in which 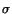$\sigma$ is the longitudinal bending stress, 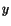$y$ the distance from the neutral axis which passes through the centroid of the cross-section and I the moment of inertia of the cross-section about the neutral axis. The derivation of (1.3.1) makes no reference to other components of stress acting at a point. Of course, if the beam were initially curved or were one interested in finding the transverse shear stress at a point, one would start essentially from scratch.