Generalized Plane Strain FEM Problem: NPIB

Submit batch job to compute stresses in a [0/45/-45/90]s "Type-I"
Graphite/Epoxy composite near the laminate "Free-Edge"

Instructions for using this form:

    1. Enter appropriate numbers in the boxes,
    2. enter your email address,
    3. click on submit, and
    4. wait for results to be returned to your email. (this will take about 20 seconds)
  1. Web location of results: edge.out and edge*.gif files will be sent to your email address.
  2. If your email does not provide direct email links, copy and paste the web address: http://www.jwave.vt.edu/output/edge_"unique date-time"/edge.html from the email into your web browser Location: window and look at this file to see if the job ran correctly.
  3. If the job ran correctly you can now download files from your web browser to your computer for archiving (a 4.6Gbyte read/write optical disk is available for each student to use in the SMVC for archiving large simulation files).
  4. If you submit the form "as-is", a sample of results has been archived in the directory: http://www.jwave.rkriz.net/output/ARCHIVE_Examples_SAVE/edge_10-23-2000-8:34:51:958/
    Select edge.html to see a summary of the results.

Below is a description of the laminate geometry and finite element grid representation used to define the "Free Edge" problem. A detailed explanation of the Laminate "Free-Edge" Problem Formulation, a comprehensive section on Finite Element Computer Program Development with instructive debug examples, and actual application using this computer program is provided for the reader. The figure below shows the laminate stacking sequence and FEM grid for a specific problem, Ref.[1]. Numbers provided in the NPIB (Network Programming Interface Builder) form below match this particular problem. Of course with the NPIB form a variety of other configurations are possible.

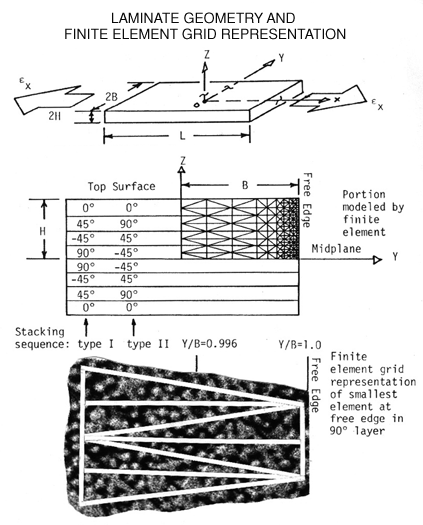
NOTE: the enlarged area showing the smallest element of the F.E.Model at the free edge is reaching the conceptual limit of the assumed homogeneous approximation ("continuum") for material properties in each element at the free edge. The finite element mesh superposed over a SEM photograph shows the heterogeneity of each graphite fiber diameter, 5 microns, is observed as a fuzzy white region. Here we are pushing the limit and assuming each element still behaves like a continuum with three fiber diameters in the z-direction and ten fiber diameters in the horizontal y-direction. For FEM elements smaller than this a continuum model can no longer be used. Instead a different model needs to be created at Y/B > 0.998 where mechanical behavior is now controlled by the individual fiber and matrix components. Hence the continuum approximation breaks down at this point.

NOTE: We have provided a complete set of ELEMENT NUMBER GRIDS below so that the student can calculate stress distributions different from the graphs shown above.

Region-D     / Region-C     / Region-B     / Region-A

Example of results shown below demonstrate the stress singularity of the stress distribution of the normal stress in the z-direction along each laminate interface. This singularity can only be accurately modeled up to Y/B=0.998 as a continuum.




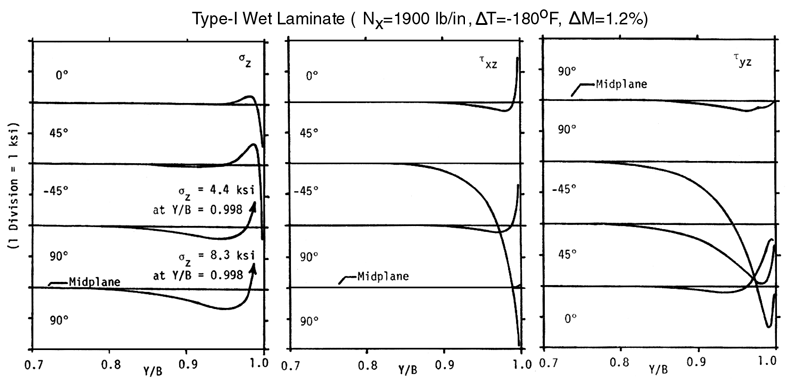
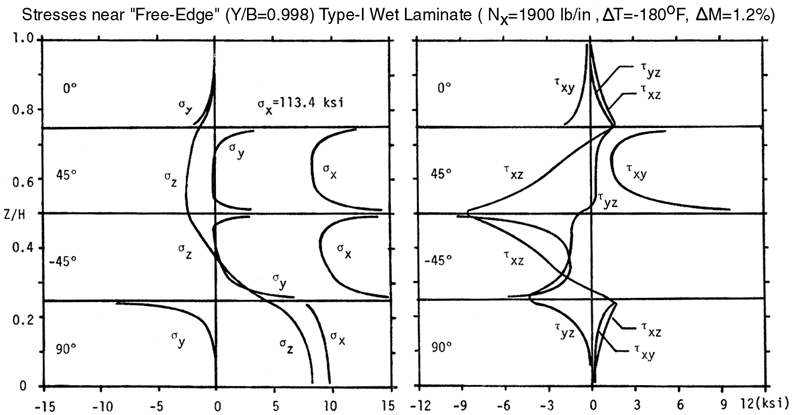
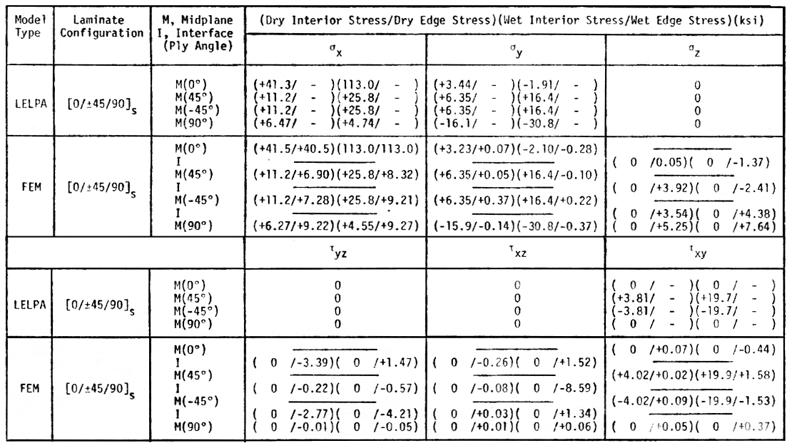
You might want to reproduce the results shown above using the "NPIB" form in the frame provided below. You will also need to use the Linear Elastic Laminated Plate Analysis (LELPA) program (module05a) which is used to convert the Nx=1900 lb./in. to a strain, e x = 0.00588 in/in, in the x-direction. The strain in the x-direction, calculated by LELPA, is then used as the out-of-plane strain normal to the H-Z plane in the form below. Notice that the sigma-z stress reverses and becomes negative ("compressive") along the +45/-45 interface and 0/+45 interface most likely because of the combination of residual stresses caused by the thermal contraction at low temperatures, Delt-T=-180F, and swelling caused by moisture absorbtion, Delta-M=1.2% moisture. The table below summarizes interior and edge stresses for two load cases: 1) DRY-FPF-Nx = 789 lb/in and 2) WET-FPF-Nx = 1900 lb/in. These WET and DRY FPF (First Ply Failures) plane loads where obtained by experimental observation, Ref.[21].

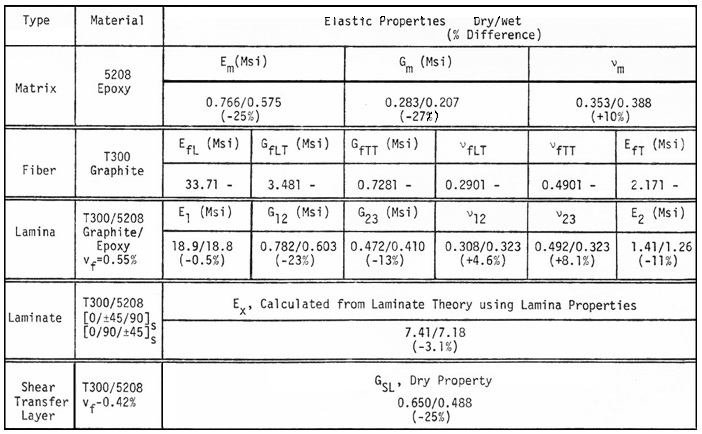
For those interested in reproducing these results you will also need the elastic and properties, see table below, used by the FEM and LELPA programs in Ref.[21].