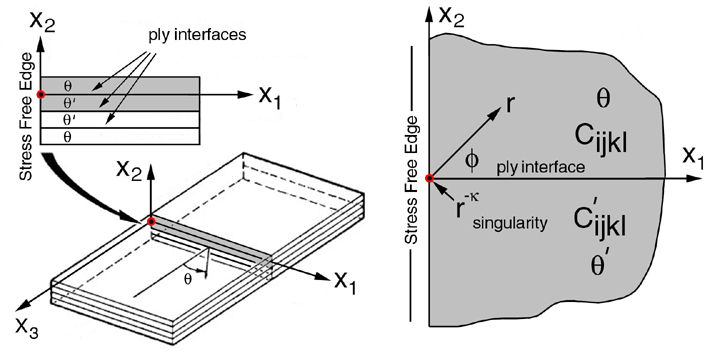
Figure 1. Coordinates defined for stress free edge singularity Ref.[25]
Instructions for using this form:
Below is a brief description of a method to calculate singuariltes that exists at an interface seperating two dissimilar anisotropic materials that terminates at a laminate stress free edge. A more complete description is give in Section 7. "Cracks Near Interfaces Between Dissimilar Anisotropic Materials"

It is important to note that singularities coincide with the coordinate system origin. Hence each interface singularity has a unique coordinate system. Since the objective here is to reproduce published results the same coordinate system established by Ting et al. will be used. For this module we have expanded on the solution introduced by Ting et al. and developed the numerical approach to solve for these singularities. The solution is organized into three parts: 1) transformation of fourth order stiffness tensor, Cijkl, for arbitrary rotation in the 1-3 plane, see eqn 35 Ref.[25], 2) calcuate eigenvalues, pk, and eigen vectors, ni and tij, from equations (9) and (10) Ref.[25], and 3) calcuate exponent, k (singularity) on radius, r, from the determinate of equations (30 and (31) of Ref.[25] using appropriate boundary conditions. From these boundary conditions 12 homogeneous equations are generated. Equation coefficients are functions of elastic properties and the exponent, k on the radius vector whose origin is located at the stress free edge where the singularity exists. With the elastic properties prescribed in the NPIB form the determinate of the coefficient matrix is only a function of the exponent, k. For comparison results from Ting et al. Ref.[25] are provided below in Table 1 using the Pipes-Pagano elastic property approximation which are the default elastic properties in the NPIB form.
| Exponent of r-k |
q'=0 | q'=90 | q'=-q |
|---|---|---|---|
| q=0 | - | 3.3388 x 10-2 | - |
| q=15 | 1.3528 x 10-4 | 3.2814 x 10-2 | 6.4322 x 10-4 |
| q=30 | 2.6286 x 10-3 | 2.8682 x 10-2 | 1.1658 x 10-2 |
| q=45 | 9.6461 x 10-3 | 2.0575 x 10-2 | 2.5575 x 10-2 |
| q=60 | 1.9866 x 10-2 | 1.0519 x 10-2 | 2.3346 x 10-2 |
| q=75 | 2.9388 x 10-2 | 2.6785 x 10-3 | 8.9444 x 10-3 |
| q=90 | 3.3388 x 10-2 | - | - |