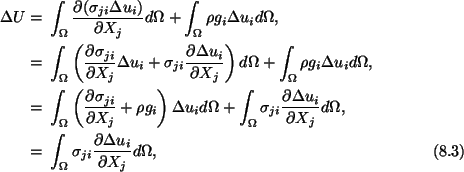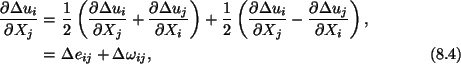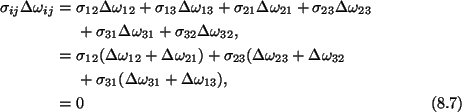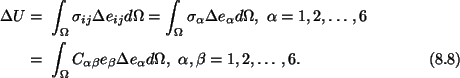

Next: Principle of Minimum Potential
Up: No Title
Previous: Boundary Conditions
Recall that we have two types of forces acting on a continuous body: surface
tractions acting on the boundary and body forces acting at every interior
point of the body. Thus during an incremental displacement
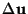 of the body, the incremental work,
of the body, the incremental work, 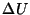 , done by external forces is
given by
, done by external forces is
given by
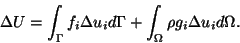 |
(8.1) |
Here
f is the surface traction (force/area) acting
at a point on the boundary 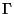 of the body
of the body 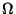 and
g is
the gravitational constant. If nonzero displacements are prescribed on a part
of the boundary
and
g is
the gravitational constant. If nonzero displacements are prescribed on a part
of the boundary 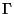 , then
f represents the reactions, i.e.,
forces exerted by the loading device on the body. Substitution for
f from (7.2) into (8.1) gives
, then
f represents the reactions, i.e.,
forces exerted by the loading device on the body. Substitution for
f from (7.2) into (8.1) gives
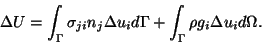 |
(8.2) |
Using the Divergence Theorem,
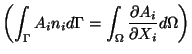 ,
we obtain
,
we obtain
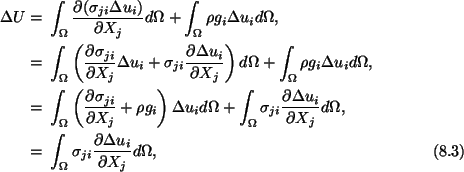
where we have also used the chain rule of differentiating the
product of two functions, and equation (3.11). We now write
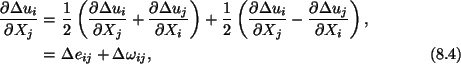
where
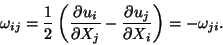 |
(8.5) |
Thus
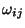 is skew symmetric which implies that
is skew symmetric which implies that
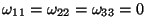 ,
,
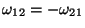 ,
,
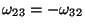 , and
, and
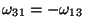 . Relation
(8.4) implies that
. Relation
(8.4) implies that
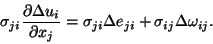 |
(8.6) |
Note that each term in (8.6) represents the sum of nine terms
since indices i and j are repeated. The skew symmetry of
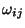 gives
gives
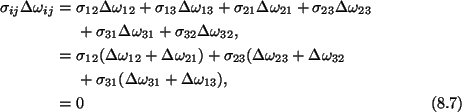
where we have used the symmetry
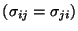 of
of
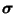 . Substitution from (8.6) and (8.7) into (8.3) gives
. Substitution from (8.6) and (8.7) into (8.3) gives
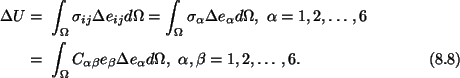
Thus
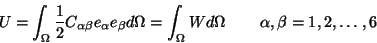 |
(8.9) |
where
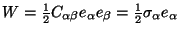 is called the strain-energy density (strain
energy/volume). U equals the total energy stored in the body. For an
elastic body, the work done by external forces equals the strain energy of the
body. Note that
is called the strain-energy density (strain
energy/volume). U equals the total energy stored in the body. For an
elastic body, the work done by external forces equals the strain energy of the
body. Note that
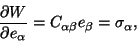 |
(8.10) |
where we have used the symmetry of the
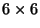 matrix
C. Thus W serves as the potential for stresses.
matrix
C. Thus W serves as the potential for stresses.


Next: Principle of Minimum Potential
Up: No Title
Previous: Boundary Conditions
Norma Guynn
1998-09-09
![]() of the body, the incremental work,
of the body, the incremental work, ![]() , done by external forces is
given by
, done by external forces is
given by
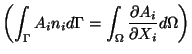 ,
we obtain
,
we obtain