

Next: A Uniqueness Theorem
Up: No Title
Previous: Work done by External
Let a body be in equilibrium under the action of specified body forces and
surface tractions. The surface tractions are prescribed over a part
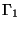 of the boundary, and on the remainder part
of the boundary, and on the remainder part
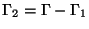 the displacements are assigned. Let
u denote the
displacement of the body in the equilibrium state.
the displacements are assigned. Let
u denote the
displacement of the body in the equilibrium state.
Consider a class of arbitrary displacements
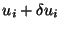 where
where
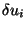 vanishes on
vanishes on 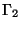 , and
, and
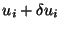 result in infinitesimal
strains in the body. Displacements
result in infinitesimal
strains in the body. Displacements
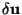 are called
virtual. The virtual work
are called
virtual. The virtual work 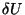 done by external forces fi and
gi in a virtual displacement
done by external forces fi and
gi in a virtual displacement
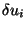 is given by
is given by
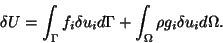 |
(9.1) |
During the virtual displacement of the body, the forces fiand gi are assumed to remain unchanged. Thus
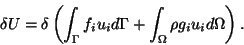 |
(9.2) |
Combining this with (8.9) we obtain
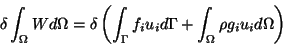 |
(9.3) |
or
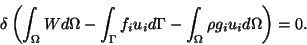 |
(9.4) |
That is, during an admissible virtual displacement of the body
the expression in parentheses has a stationary value. The quantity
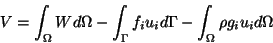 |
(9.5) |
is called the potential energy of the body, and (9.4) implies that
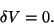 |
(9.6) |
Since the displacements ui were assumed to correspond to an
equilibrium state, therefore V takes on a stationary value when the
displacements
u are for a state of equilibrium. Actually, the
following stronger result holds.
Principle of Minimum Potential Energy: Of all displacements
satisfying the given boundary conditions those which satisfy the equilibrium
equations make the potential energy an absolute minimum.
We will use this principle to find an equilibrium configuration of the body by
the finite element method.


Next: A Uniqueness Theorem
Up: No Title
Previous: Work done by External
Norma Guynn
1998-09-09
![]() of the boundary, and on the remainder part
of the boundary, and on the remainder part
![]() the displacements are assigned. Let
u denote the
displacement of the body in the equilibrium state.
the displacements are assigned. Let
u denote the
displacement of the body in the equilibrium state.
![]() where
where
![]() vanishes on
vanishes on ![]() , and
, and
![]() result in infinitesimal
strains in the body. Displacements
result in infinitesimal
strains in the body. Displacements
![]() are called
virtual. The virtual work
are called
virtual. The virtual work ![]() done by external forces fi and
gi in a virtual displacement
done by external forces fi and
gi in a virtual displacement
![]() is given by
is given by