A Uniqueness Theorem

The solution of the boundary value problem

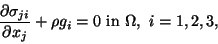$$\frac{\partial\sigma_{ji}}{\partial x_j} + \rho g_i = 0\ {\rm in}\ \Omega,\ i = 1,2,3, \tag{10.1}$$ (10.1)

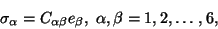$$\sigma_\alpha = C_{\alpha\beta}e_\beta,\ \alpha,\beta = 1,2,\ldots , 6, \tag{10.2}$$ (10.2)

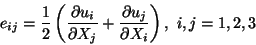$$e_{ij} = \frac{1}{2}\left(\frac{\partial u_i}{\partial X_j} + \frac{\partial u_j}{\partial X_i}\right),\ i,j = 1,2,3 \tag{10.3}$$ (10.3)

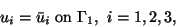$$u_i = \bar u_i\ {\rm on}\ \Gamma_1,\ i = 1,2,3,\tag{10.4}$$ (10.4)

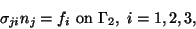$$\sigma_{ji}n_j = f_i\ {\rm on}\ \Gamma_2,\ i = 1,2,3,\tag{10.5}$$ (10.5)

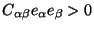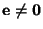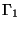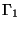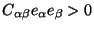is unique provided that $C_{\alpha\beta}e_\alpha e_\beta > 0$ for every $\mathbf{e}\ne \mathbf{0}$, and $\Gamma_1$ is not empty. If $\Gamma_1$ is empty, then the solution is unique only to within a rigid body motion. For an isotropic linear elastic material, the condition $C_{\alpha\beta}e_\alpha e_\beta > 0$ is equivalent to 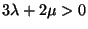$3\lambda + 2\mu > 0$ and $\mu >0$.

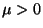A consequence of this uniqueness theorem is that if a solution of equations (10.1)-(10.5) has been found by any means, then it is the only solution of the problem.