

Next: Bending of Beams by
Up: No Title
Previous: A Uniqueness Theorem
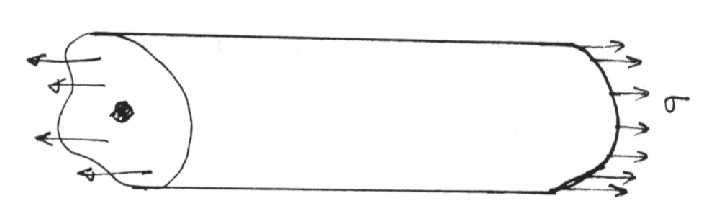
For simplicity we consider a uniform prismatic bar made of a homogeneous and
isotropic linear elastic material with its mantle free of surface tractions.
One end of the bar is loaded by uniformly distributed surface traction,
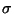 , acting along the axis of the bar, the centroid of the other end is
rigidly clamped to prevent rigid motion of the bar, and the clamped end is
loaded to keep the bar in equilibrium. A sketch of the problem studied is
shown in Fig. 11.1
, acting along the axis of the bar, the centroid of the other end is
rigidly clamped to prevent rigid motion of the bar, and the clamped end is
loaded to keep the bar in equilibrium. A sketch of the problem studied is
shown in Fig. 11.1
The stress field
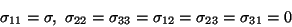 |
(11.1) |
identically satisfies the equations of equilibrium
when gravitational
forces are neglected. Also, the traction boundary
conditions on the mantle and the loaded end are satisfied. From Hooke's law
(6.3) with
C given by (6.4),
we obtain
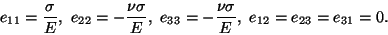 |
(11.2) |
Therefore
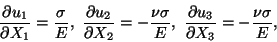 |
(11.3) |
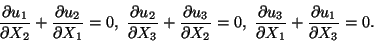 |
(11.4) |
An integration of equations (11.3) gives
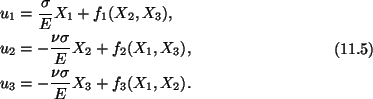
Substitution from (10.5) into (10.4) yields
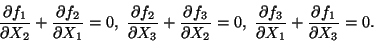 |
(11.6) |
Recalling that f1 is a function of X2 and X3, f2 is
a function of X1 and X3, and f3 is a function of X1,X2, we
conclude from (11.6) that
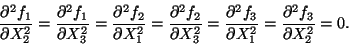 |
(11.7) |
Hence
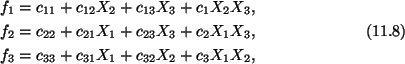
where
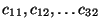 ,
, 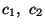 and c3 are constants.
We now substitute from (11.8) into (11.6) to obtain
and c3 are constants.
We now substitute from (11.8) into (11.6) to obtain
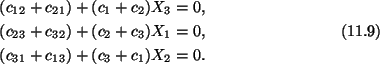
Since these equations must hold for all points in the interior of
the bar, therefore
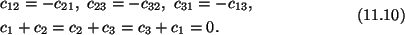
The second set of equations (11.10) gives
|
c1 = c2 = c3 = 0.
|
(11.11) |
Substitution from (11.8), (11.10) and (11.11) into (11.5) gives
the following expressions for the displacement field in the bar.
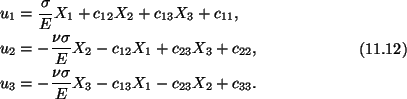
Since
u1 = u2 = u3 = 0 at the centroid
X1 = X2 = X3 = 0of the bar, therefore, we conclude from (11.12) that
|
c11 = c22 = c33 = 0.
|
(11.13) |
In order to eliminate rigid rotations of the bar,
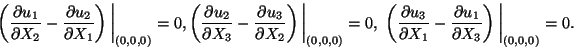 |
(11.14) |
That is, a small region around the centroid of the
cross-section at X3 = 0 is rigidly clamped. Equations (11.12) and (11.14)
give
|
c12 = c13 = c23 = 0.
|
(11.15) |
Thus, the displacement field in the bar is given by
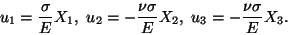 |
(11.16) |
If the diameter of the cross-section of the bar is much smaller than the
length of the bar, then the maximum values of u2 and u3 will be
considerably smaller than the maximum value of u1. In such cases, we
neglect changes in the cross-section of the bar and focus on finding u1only.
Consider a bar for which the Young's modulus is a function of X1, and a
typical dimension in the cross-section is much smaller than the length of the
bar. We will neglect lateral deformations of the cross-section and find u1
= u only as a function of X1 = X. Equations for finding the function uare
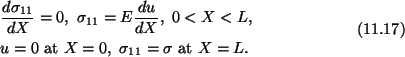
Substitutiion for
 in terms of u gives
in terms of u gives
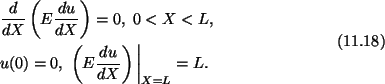
If E as a function of X is known, then we can integrate the
second-order ordinary differential equation (11.18)1 and solve for u.
However, when the functional relationship between E and X is complicated,
one may not be able to analytically
integrate (11.18)1. We now discuss the finite
element method of solving the problem defined by (11.18).
Boundary condition (11.18)2 is called essential, and (11.18)3 natural.
Instead of directly solving eqn. (11.18) we will first derive the potential
energy of the system and find a solution by minimizing the potential energy.
As shown in Section 9, the potential energy is minimum in the equilibrium
configuration. This approach is being followed to stay consistent with the
earlier lectures in this course.
Strain energy of the bar is given by
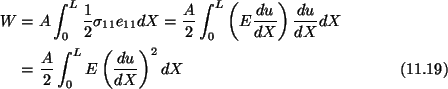
where A is the cross-section of the bar. Since the end X = 0is fixed, therefore, for the potential energy, V, of the system we have
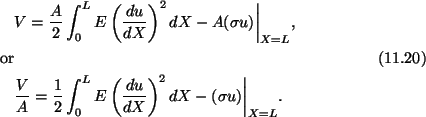
In the finite element work, we express u as a linear
combination of the finite element basis functions
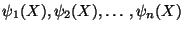 . The given domain is divided into disjoint (nonoverlapping)
subdomains, called finite elements so that their union (sum) equals the entire
domain. Thus every part of the region is counted only once. Special points
generally on the common boundary of adjoining elements are selected and called
nodes. The collection of elements and nodes is called a finite element mesh.
For the potential energy with first-order derivatives in the integrand, the
basis functions
. The given domain is divided into disjoint (nonoverlapping)
subdomains, called finite elements so that their union (sum) equals the entire
domain. Thus every part of the region is counted only once. Special points
generally on the common boundary of adjoining elements are selected and called
nodes. The collection of elements and nodes is called a finite element mesh.
For the potential energy with first-order derivatives in the integrand, the
basis functions
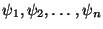 must be once differentiable
everywhere on [0,L] except possibly at a finite number of points. Thus
these functions must be continuous on [0,L].
Functions
must be once differentiable
everywhere on [0,L] except possibly at a finite number of points. Thus
these functions must be continuous on [0,L].
Functions
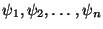 are chosen to satisfy the following
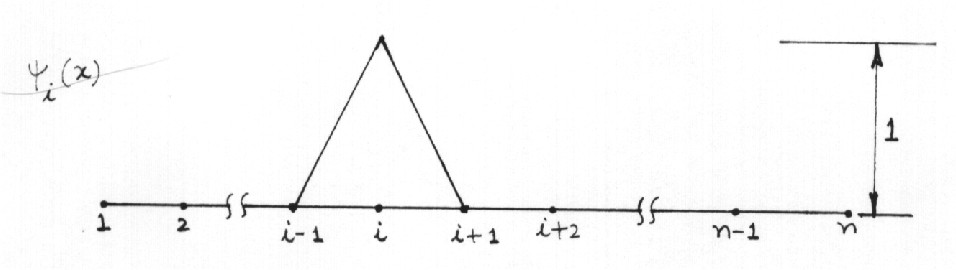
conditions: (1)
are chosen to satisfy the following
conditions: (1) 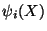 equals 1 at node i and vanishes at all other
nodes, (2)
equals 1 at node i and vanishes at all other
nodes, (2) 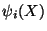 is a simple polynomial defined piecewise over the
entire domain, and (3) a constant can be expressed as a linear combination of
is a simple polynomial defined piecewise over the
entire domain, and (3) a constant can be expressed as a linear combination of
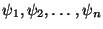 . Thus for the finite element mesh
. Thus for the finite element mesh
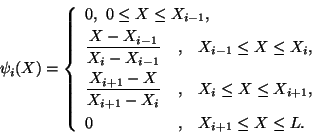 |
(11.21) |
The basis function 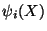 is non-zero only on the two
elements that share node i. The restriction of a basis function to an
element is called a shape function, and a basis function
is non-zero only on the two
elements that share node i. The restriction of a basis function to an
element is called a shape function, and a basis function 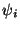 is obtained
by patching together the shape functions defined on elements meeting at node
i. Corresponding to basis functions (11.21) there are only two basis
functions which are non-zero on an element. For example, on element
is obtained
by patching together the shape functions defined on elements meeting at node
i. Corresponding to basis functions (11.21) there are only two basis
functions which are non-zero on an element. For example, on element
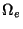 with nodes e and e + 1, only
with nodes e and e + 1, only 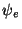 and
and
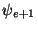 will be
non-zero;
will be
non-zero; 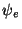 equals 1 on the left node e and zero on the right node
(e + 1) and
equals 1 on the left node e and zero on the right node
(e + 1) and
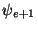 equals zero on the left node e and 1 on the
right node (e + 1). Hence there are two shape functions associated with the
element e; one with each node on the element. The shape function for node
e equals 1 at node e and zero at node e + 1, and the shape function
for node e+1 takes on values 0 and 1 respectively at nodes e and
e+1.
equals zero on the left node e and 1 on the
right node (e + 1). Hence there are two shape functions associated with the
element e; one with each node on the element. The shape function for node
e equals 1 at node e and zero at node e + 1, and the shape function
for node e+1 takes on values 0 and 1 respectively at nodes e and
e+1.
Temporarily, we ignore the boundary condition u(0) = 0 and approximate uby
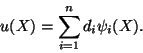 |
(11.22) |
Recalling that
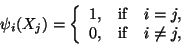 |
(11.23) |
we get
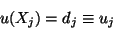 |
(11.24) |
That is, di in (11.23) equals the value of the unknown
function at node i. Substitution from (11.22) and (11.24) into (11.20)
yields
![\begin{displaymath}\frac{V}{A} = \frac{1}{2}\sum^{n-1}_{i=1}\int^{X_{i+1}}_{X_i}...
...1}_{k=1}u_k\psi_k(X)\right)\right]\bigg\vert _{X=L}\tag{11.25}
\end{displaymath}](img190.gif) |
(11.25) |
where
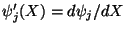 . For
. For 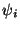 given by
(11.21),
given by
(11.21),
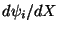 is exhibited in Fig. 11.3. The derivative
is exhibited in Fig. 11.3. The derivative
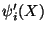 is undefined only at three points,
is undefined only at three points,
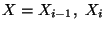 and
Xi+1.
and
Xi+1.
Therefore, the integral on the right-hand side of (11.25) can be
evaluated. After the other expression on the right-hand side of (11.25) has
also been evaluated, V becomes a function of n variables, viz.,
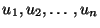 . The stationary points of V are given by
. The stationary points of V are given by
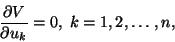 |
(11.26) |
or
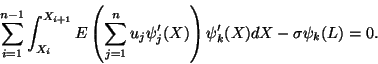 |
(11.27) |
With the notations
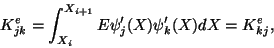 |
(11.28) |
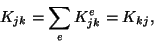 |
(11.29) |
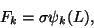 |
(11.30) |
we can write (11.27) as
To see if the stationary points given by (11.26) or
equivalently a solution of (11.31) minimizes V, we need to examine the
second-order derivatives. Note that
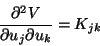 |
(11.32) |
and once u(0) = 0 has been used, the matrix
Kis positive
definite. Thus, indeed the solution of (11.31) minimizes the potential energy
V and corresponds to an equilibrium configuration of the body.
The matrix
Ke is called the element stiffness matrix, and
K the global stiffness matrix. The vector
Fis the load vector.
For the present problem,
Fhas a contribution only from the applied load at
the end x = L. This is evidenced by 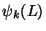 equalling 1 only when k =
n, and zero otherwise.
equalling 1 only when k =
n, and zero otherwise.
We now impose the boundary condition u1 = 0 or u(0) = 0. One way to
accomplish this is to delete the first row and first column of the matrix
K, and the first row of
F, and then solve (11.31) for
the remaining unknowns
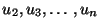 . The other technique is to add a
big number B to K11 and Bu(0) to the first column of
F,
and then
solve (11.31) for
. The other technique is to add a
big number B to K11 and Bu(0) to the first column of
F,
and then
solve (11.31) for
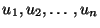 . In this case the boundary condition
u(0) = 0 is approximately satisfied. Knowing
. In this case the boundary condition
u(0) = 0 is approximately satisfied. Knowing
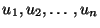 , the
displacement u at any point in the bar is found from
, the
displacement u at any point in the bar is found from
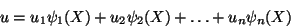 |
(11.33) |
where
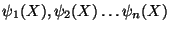 are the known
finite element basis functions. One can compute the axial strain
are the known
finite element basis functions. One can compute the axial strain
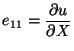 from (11.33)
and then the axial stress
from (11.33)
and then the axial stress
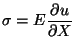 at any point in the bar. Since the basis
functions
at any point in the bar. Since the basis
functions
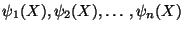 are not differentiable at
the node points, therefore strains and stresses can not be computed there.
Stresses are computed at points interior to an element, and are extrapolated
to nodes if needed.
are not differentiable at
the node points, therefore strains and stresses can not be computed there.
Stresses are computed at points interior to an element, and are extrapolated
to nodes if needed.
The basis functions shown in Fig. 11.2 are polynomials of order one in x.
These are lowest order polynomials that can be used to solve the present
problem. However, higher order polynomials defined piecewise over the domain
that are continuous across neighboring elements will work too, and will
usually give a better representation of the axial stress than that obtained
with polynomials (11.21). Another way to improve the accuracy of the solution
is to use a finer mesh, i.e., reduce the size of the elements.


Next: Bending of Beams by
Up: No Title
Previous: A Uniqueness Theorem
Norma Guynn
1998-09-09
![]() , acting along the axis of the bar, the centroid of the other end is
rigidly clamped to prevent rigid motion of the bar, and the clamped end is
loaded to keep the bar in equilibrium. A sketch of the problem studied is
shown in Fig. 11.1
, acting along the axis of the bar, the centroid of the other end is
rigidly clamped to prevent rigid motion of the bar, and the clamped end is
loaded to keep the bar in equilibrium. A sketch of the problem studied is
shown in Fig. 11.1

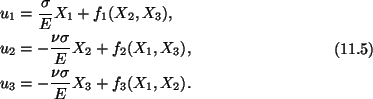
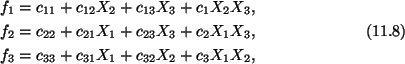
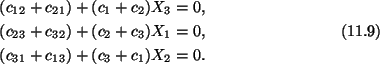
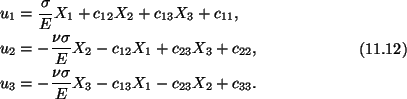
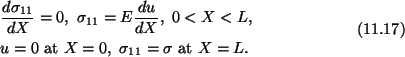
![]() in terms of u gives
in terms of u gives
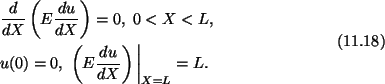
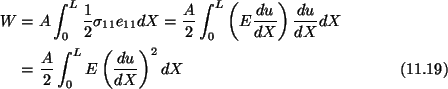
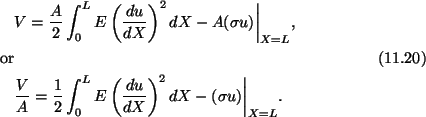
![]() . The given domain is divided into disjoint (nonoverlapping)
subdomains, called finite elements so that their union (sum) equals the entire
domain. Thus every part of the region is counted only once. Special points
generally on the common boundary of adjoining elements are selected and called
nodes. The collection of elements and nodes is called a finite element mesh.
For the potential energy with first-order derivatives in the integrand, the
basis functions
. The given domain is divided into disjoint (nonoverlapping)
subdomains, called finite elements so that their union (sum) equals the entire
domain. Thus every part of the region is counted only once. Special points
generally on the common boundary of adjoining elements are selected and called
nodes. The collection of elements and nodes is called a finite element mesh.
For the potential energy with first-order derivatives in the integrand, the
basis functions
![]() must be once differentiable
everywhere on [0,L] except possibly at a finite number of points. Thus
these functions must be continuous on [0,L].
Functions
must be once differentiable
everywhere on [0,L] except possibly at a finite number of points. Thus
these functions must be continuous on [0,L].
Functions
![]() are chosen to satisfy the following
conditions: (1)
are chosen to satisfy the following
conditions: (1) ![]() equals 1 at node i and vanishes at all other
nodes, (2)
equals 1 at node i and vanishes at all other
nodes, (2) ![]() is a simple polynomial defined piecewise over the
entire domain, and (3) a constant can be expressed as a linear combination of
is a simple polynomial defined piecewise over the
entire domain, and (3) a constant can be expressed as a linear combination of
![]() . Thus for the finite element mesh
. Thus for the finite element mesh

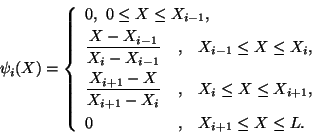
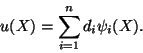
![\begin{displaymath}\frac{V}{A} = \frac{1}{2}\sum^{n-1}_{i=1}\int^{X_{i+1}}_{X_i}...
...1}_{k=1}u_k\psi_k(X)\right)\right]\bigg\vert _{X=L}\tag{11.25}
\end{displaymath}](img190.gif)
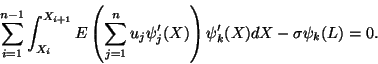
![]() equalling 1 only when k =
n, and zero otherwise.
equalling 1 only when k =
n, and zero otherwise.
![]() . The other technique is to add a
big number B to K11 and Bu(0) to the first column of
F,
and then
solve (11.31) for
. The other technique is to add a
big number B to K11 and Bu(0) to the first column of
F,
and then
solve (11.31) for
![]() . In this case the boundary condition
u(0) = 0 is approximately satisfied. Knowing
. In this case the boundary condition
u(0) = 0 is approximately satisfied. Knowing
![]() , the
displacement u at any point in the bar is found from
, the
displacement u at any point in the bar is found from
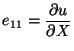 from (11.33)
and then the axial stress
from (11.33)
and then the axial stress
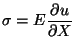 at any point in the bar. Since the basis
functions
at any point in the bar. Since the basis
functions