Concept of Strain

Consider a bar of axial length L in the reference configuration. Because of applying either a temperature change, axial force or an electric/magnetic field, let its length change to $\ell$. Then

$$\mbox{average axial strain} = \frac{\ell - L}{L}.\tag{4.1}$$ (4.1)

If $\ell > L$, the axial strain is tensile, otherwise it is compressive.

Envisage the twisting of a circular bar fixed at one end. The change in the angle between two mutually perpendicular line elements passing through a point is called the shear strain. In Fig. 4.1,

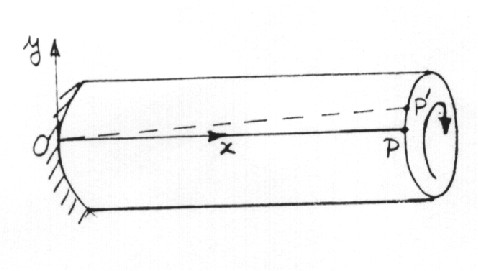
$$\mbox{shear strain at point}\ O = \gamma . \tag{4.2}$$ (4.2)

Positive values of $\gamma$ imply that the angle between the deformed positions of the two lines is less than $\pi /2$.

We now generalize definitions (4.1) and (4.2) to three-dimensional deformation of a body. Infinitely many lines pass through any point Q in the body and there are infinitely many pairs of mutually perpendicular lines through Q. The first question is how to denote the axial strain along these lines and what notation to use for the shear strain between mutually perpendicular pairs of lines through Q? We use suffixes to indicate the direction of line elements passing through Q. Thus e_xx,e_yy,e_zz denote axial strains along $x,\ y$ and z axes respectively and $e_{xy},\ e_{yz}$ and e_zx denote shear strains between lines parallel to x and y, y and z, and z and x axes respectively. For a line element parallel to a unit vector M the axial strain will be denoted by e_MM, and the shear strain between two mutually perpendicular line elements parallel to unit vectors M and Nwill be denoted by e_MN. The second question is: through point Q, along how many lines do we need to know the axial strain, and between how many pairs of mutually perpendicular lines do we need to know the shear strain so that we can find the axial strain along any line through Qand the shear strain between any two mutually perpendicular lines through Q? The answer is: three mutually perpendicular lines. Note the similarity between this answer and the one for stresses in Section 2. The result for strains is proved below.