

Next: Material Characterization
Up: No Title
Previous: Concept of Strain
Notation. It is convenient to use the index notation.
Co-ordinate axes 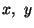 and z will henceforth be denoted by
and z will henceforth be denoted by 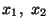 and x3 respectively. Co-ordinates of a point in the reference
configuration will be denoted by
X1,X2,X3, and those in the present
configuration by
x1,x2,x3. Components of a vector
A will
be denoted by
A1,A2,A3 rather than by
and x3 respectively. Co-ordinates of a point in the reference
configuration will be denoted by
X1,X2,X3, and those in the present
configuration by
x1,x2,x3. Components of a vector
A will
be denoted by
A1,A2,A3 rather than by 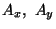 and Az. Thus
and Az. Thus
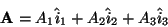 |
(5.1) |
where
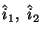 and
and 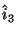 are unit vectors
along
are unit vectors
along 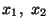 and x3 axes respectively. We shall also adopt the
following summation convention: a repeated index implies summation over
the range of the index. That is, an index appearing twice (not more) in a
term implies
the sum of terms. Thus the inner product between two vectors
A and
B can be written as
and x3 axes respectively. We shall also adopt the
following summation convention: a repeated index implies summation over
the range of the index. That is, an index appearing twice (not more) in a
term implies
the sum of terms. Thus the inner product between two vectors
A and
B can be written as
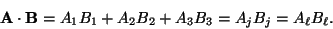 |
(5.2) |
Note that the repeated index is dummy. Recall that
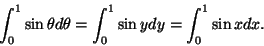 |
(5.3) |
Thus, the repeated index in (5.2) plays the same role as the
variable of integration does in (5.3).
Due to the application of loads to the body, let points
P(X1,X2,X3) and
Q(X1 + dX1,X2 + dX2,X3 + dX3) in the reference configuration move to
places
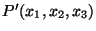 and
and
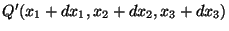 in the present configuration. We assume that different material
particles always occupy distinct places. Thus collisions between any two
material
particles
are not allowed. A consequence of this assumption is that
x1,x2,x3 are
single-valued functions of
X1,X2,X3. The displacement vector
u of point P is defined by
in the present configuration. We assume that different material
particles always occupy distinct places. Thus collisions between any two
material
particles
are not allowed. A consequence of this assumption is that
x1,x2,x3 are
single-valued functions of
X1,X2,X3. The displacement vector
u of point P is defined by
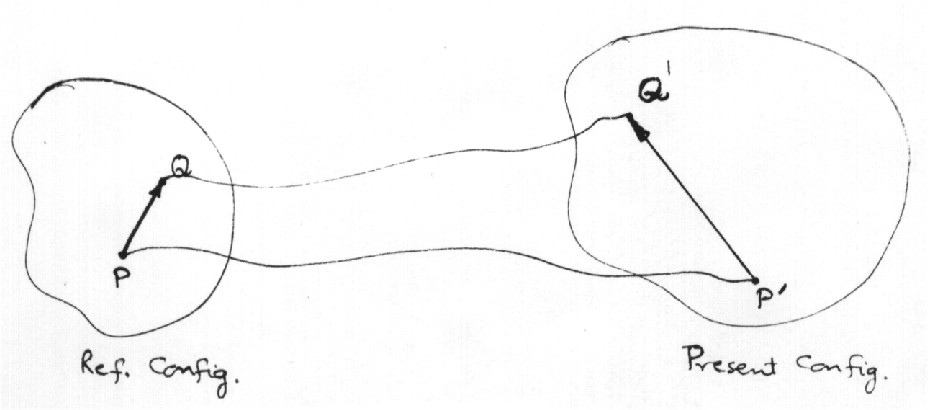
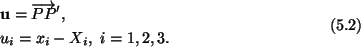
Thus  and u3 are components of
and u3 are components of
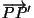 along
along 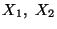 and X3 axes. Note that
and X3 axes. Note that
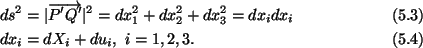
We now assume that
u1,u2,u3 are single-valued continuously
differentiable functions of
X1,X2,X3. Hence
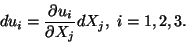 |
(5.5) |
Assuming that the displacement gradients are small, i.e.,.
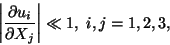 |
(5.6) |
we obtain
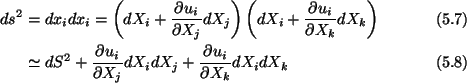
where we have neglected the term quadratic in
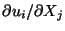 because of
(5.6). In the second and third terms on the right-hand side of (5.8), there
are two repeated indices. Thus, each term represents the sum of nine
terms. Since
because of
(5.6). In the second and third terms on the right-hand side of (5.8), there
are two repeated indices. Thus, each term represents the sum of nine
terms. Since
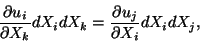 |
(5.9) |
equation (5.8) can be rewritten as
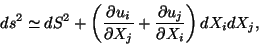 |
(5.10) |
or
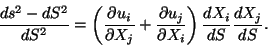 |
(5.11) |
With the notations
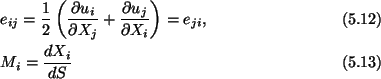
we rewrite (5.11) as
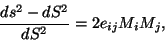 |
(5.14) |
and
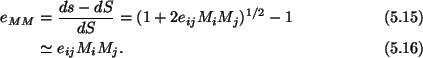
Note that
M is a unit vector along
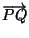 , and
eMM is the axial strain in the direction of
, and
eMM is the axial strain in the direction of
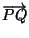 .
Equation (5.16) expresses the axial strain, eMM , along any direction
M in terms of the components
e11,e22,e33,e12,e23,e31 of the strain and the unit vector
M.
.
Equation (5.16) expresses the axial strain, eMM , along any direction
M in terms of the components
e11,e22,e33,e12,e23,e31 of the strain and the unit vector
M.
Let
M = (1,0,0) be a unit vector along X1-axis. It follows
from (5.16) and (5.12) that
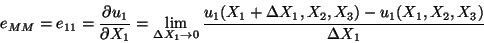 |
(5.17) |
where the last equality follows from the definition of a
partial
derivative. Thus e11 equals the change in length per unit length of an
infinitesimal line element passing through P and parallel to X1-axis.
Similar interpretations hold for e22 and e33.
Now consider two mutually perpendicular infinitesimal vectors
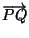 and
and
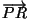 passing through P which are
deformed into
passing through P which are
deformed into
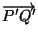 and
and
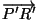 respectively. From (5.4) and (5.5),
respectively. From (5.4) and (5.5),
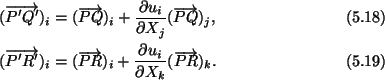
The angle 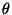 between
between
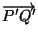 and
and
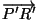 is given by
is given by
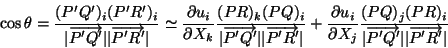 |
(5.20) |
where we have used
(PQ)i(PR)i = 0, and neglected the
quadratic terms in
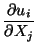 since the
displacement gradients have been assumed to be infinitesimal.
Recalling that deformations, i.e., the change in length/length and the changes
in angles, measured in radians, between any two mutually perpendicular
line elements
are small,
since the
displacement gradients have been assumed to be infinitesimal.
Recalling that deformations, i.e., the change in length/length and the changes
in angles, measured in radians, between any two mutually perpendicular
line elements
are small,
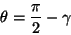 |
(5.21) |
where 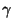 is the shear strain between
is the shear strain between
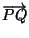 and
and
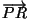 . Equations (5.20) and (5.21)
yield
. Equations (5.20) and (5.21)
yield
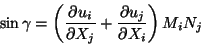 |
(5.22) |
or
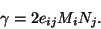 |
(5.23) |
Equation (5.23) expresses the shear strain in terms of
e11,e22,e33,e12,e23,e31 and the unit vectors
Mand
N.
Equations (5.16) and (5.23) prove the following result: axial strains along
three mutually perpendicular lines passing through a point P and shear
strains between them determine the axial strain along any line through P and
the shear strain between any two mutually perpendicular lines through P.
These relations are the three-dimensional analogs of the two dimensional
strain transformation equations derived in the first course on Mechanics of
Deforms.
There one generally uses Mohr's circle to find the axial strain along any line
from the known strain state along two mutually perpendicular lines.


Next: Material Characterization
Up: No Title
Previous: Concept of Strain
Norma Guynn
1998-09-09
![]() and z will henceforth be denoted by
and z will henceforth be denoted by ![]() and x3 respectively. Co-ordinates of a point in the reference
configuration will be denoted by
X1,X2,X3, and those in the present
configuration by
x1,x2,x3. Components of a vector
A will
be denoted by
A1,A2,A3 rather than by
and x3 respectively. Co-ordinates of a point in the reference
configuration will be denoted by
X1,X2,X3, and those in the present
configuration by
x1,x2,x3. Components of a vector
A will
be denoted by
A1,A2,A3 rather than by ![]() and Az. Thus
and Az. Thus
![]() and
and
![]() in the present configuration. We assume that different material
particles always occupy distinct places. Thus collisions between any two
material
particles
are not allowed. A consequence of this assumption is that
x1,x2,x3 are
single-valued functions of
X1,X2,X3. The displacement vector
u of point P is defined by
in the present configuration. We assume that different material
particles always occupy distinct places. Thus collisions between any two
material
particles
are not allowed. A consequence of this assumption is that
x1,x2,x3 are
single-valued functions of
X1,X2,X3. The displacement vector
u of point P is defined by

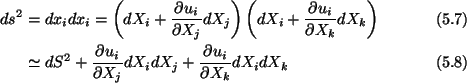
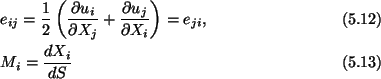
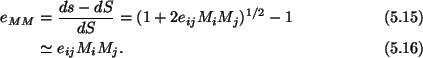
![]() and
and
![]() passing through P which are
deformed into
passing through P which are
deformed into
![]() and
and
![]() respectively. From (5.4) and (5.5),
respectively. From (5.4) and (5.5),
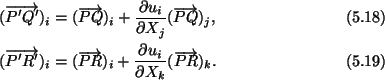
![]() between
between
![]() and
and
![]() is given by
is given by