Consider two sets of rectangular Cartesian frames of reference
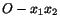 and
and
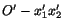 in a plane. If the frame of reference
in a plane. If the frame of reference
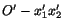 is obtained from
is obtained from
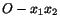 by a shift of
the origin without a change in orientation, then, the transformation is a
translation.
by a shift of
the origin without a change in orientation, then, the transformation is a
translation.
If a point 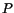 has coordinates
has coordinates 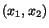 and
and
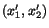 with respect to
with respect to 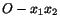 and
and
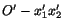 respectively and
respectively and 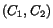 are the
coordinates of
are the
coordinates of 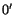 with respect to
with respect to
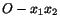 , then
, then
or briefly
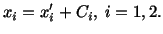 |
(2.7.1) |
If the origin remains fixed, and the new axes
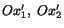 are
obtained by rotating
are
obtained by rotating 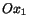 and
and 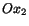 through an angle
through an angle 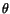 in the
counter-clockwise direction, then
in the
counter-clockwise direction, then
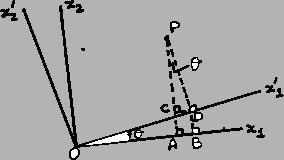
the transformation of axes is a rotation. Let the point
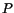 have coordinates
have coordinates 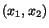 and
and
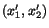 relative
to
relative
to
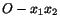 and
and
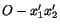 respectively. Then,
respectively. Then,
We can write
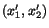 in terms of
in terms of 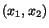 as
as
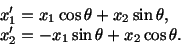 |
(2.7.2) |
Using the index notation, the set of
eqns. (2.7.2) can be written as
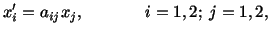 |
(2.7.3) |
where 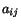 are elements of the matrix
are elements of the matrix ![$ [a_{ij}]$](img201.gif) ;
;
Before we generalize (2.7.1) and (2.7.2) to three dimensions we
give below an alternate method of arriving at (2.7.2). Let
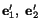 denote unit
vectors along
denote unit
vectors along
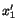 and
and
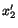 -axes
and
-axes
and
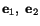 unit vectors along
unit vectors along 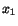 and
and 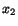 -axes.
Then
-axes.
Then
Also
Therefore,
This latter approach can more easily be adopted to the
3-dimensional case. If the primed axes
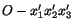 are obtained from the unprimed axes
are obtained from the unprimed axes
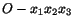 just by a translation, then
the coordinates of a point with respect to the two sets of axes are related by
(2.7.1) wherein the index
just by a translation, then
the coordinates of a point with respect to the two sets of axes are related by
(2.7.1) wherein the index 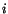 ranges from
ranges from 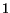 to
to 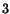 . Now let us assume that
the primed axes are obtained from the unprimed axes by a rotation only. Let
us denote unit vectors along
. Now let us assume that
the primed axes are obtained from the unprimed axes by a rotation only. Let
us denote unit vectors along
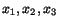 by
by
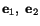 , and
, and
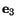 respectively
and those along
respectively
and those along
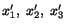 by
by
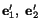 and
and
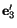 respectively. If
respectively. If
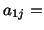 cosine of the angle between cosine of the angle between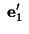 and and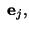 |
|
then
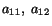 and
and 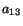 are the direction cosines of
are the direction cosines of
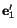 with respect to the unprimed axes. We can write
with respect to the unprimed axes. We can write
Similarly,
Or
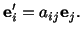 |
(2.7.4) |
Note that the matrix 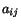 is
is 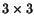 . Since
. Since
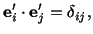 |
(2.7.5) |
therefore,
Equations (2.7.6) are equivalent to the following six equations.
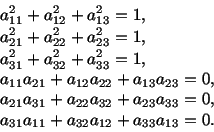 |
(2.7.7) |
The first three equations are equivalent to the statement
that
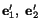 and
and
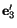 are unit vectors; the last
three equations are equivalent to the statement that
are unit vectors; the last
three equations are equivalent to the statement that
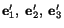 are mutually orthogonal.
Of course, we can
write
are mutually orthogonal.
Of course, we can
write
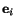 's in terms of
's in terms of
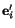 's. Since
's. Since
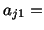 cosine of the angle between cosine of the angle between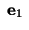 and and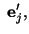 |
|
therefore,
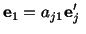 or or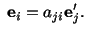 |
(2.7.8) |
From the point of view of the solution of a set of simultaneous
linear equations, the matrix 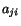 in (2.7.8) must be identified as the
inverse of the matrix
in (2.7.8) must be identified as the
inverse of the matrix 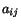 :
:
![$\displaystyle [a_{ij}]^{-1} = [a_{ji}] = [a_{ij}]^T.$](img252.gif) |
(2.7.9) |
Here
![$ [a_{ij}]^T$](img253.gif) is the transpose of the matrix
is the transpose of the matrix ![$ [a_{ij}]$](img201.gif) . A
matrix
. A
matrix ![$ [a_{ij}]$](img201.gif) , which satisfies eqn. (2.7.9) is called an orthogonal
matrix. That is, the transpose of an orthogonal matrix equals its inverse. A
transformation is said to be orthogonal if the associated matrix is
orthogonal. The matrix
, which satisfies eqn. (2.7.9) is called an orthogonal
matrix. That is, the transpose of an orthogonal matrix equals its inverse. A
transformation is said to be orthogonal if the associated matrix is
orthogonal. The matrix ![$ [a_{ij}]$](img201.gif) in (2.7.4) defining a rotation of
coordinate axes is orthogonal.
in (2.7.4) defining a rotation of
coordinate axes is orthogonal.
For an orthogonal matrix we have
Therefore
and thus
An orthogonal matrix whose determinant equals 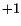 is called
proper orthogonal and the one whose determinant equals
is called
proper orthogonal and the one whose determinant equals 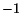 is called
improper orthogonal. A proper orthogonal matrix transforms a
right-handed triad of axes into a right-handed set of axes whereas an improper
orthogonal matrix transforms a right-handed set of axes into a left-handed set
of axes or vice-versa.
is called
improper orthogonal. A proper orthogonal matrix transforms a
right-handed triad of axes into a right-handed set of axes whereas an improper
orthogonal matrix transforms a right-handed set of axes into a left-handed set
of axes or vice-versa.
Exercise: Consider a cube formed by the orthonormal
vectors
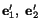 and
and
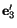 . By setting the volume of this
cube equal to 1, show that
. By setting the volume of this
cube equal to 1, show that
![$ {\rm det}[a_{ij}] = 1$](img261.gif) .
.
Consider a vector
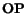 emanating from the origin
emanating from the origin 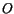 and
ending at a point
and
ending at a point 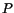 . With respect to the primed and unprimed axes,
. With respect to the primed and unprimed axes,
Similarly,
Example: The components of a vector
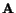 with
respect to
unprimed axes are
with
respect to
unprimed axes are
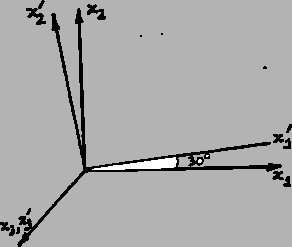
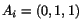 . Consider a set of primed
coordinate axes obtained by rotating the unprimed axes through an angle of
. Consider a set of primed
coordinate axes obtained by rotating the unprimed axes through an angle of
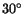 about the
about the 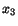 -axis (see Fig. ). What are the components,
-axis (see Fig. ). What are the components,
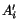 , of this vector with respect to the primed set of axes?
, of this vector with respect to the primed set of axes?
Solution:
Therefore
Now
can be written as
Hence
Summarizing our discussion of the transformation of coordinate axes, we note
that a general transformation from unprimed to primed axes combines both a
translation and a rotation of the axes. This can be written as
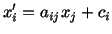 |
(2.7.10) |
where 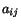 is an orthogonal matrix and
is an orthogonal matrix and 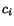 is a constant.
Under this transformation, the components of a vector
is a constant.
Under this transformation, the components of a vector
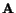 in the
two sets of axes are related as
in the
two sets of axes are related as
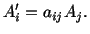 |
(2.7.11) |
![]() and
and
![]() in a plane. If the frame of reference
in a plane. If the frame of reference
![]() is obtained from
is obtained from
![]() by a shift of
the origin without a change in orientation, then, the transformation is a
translation.
by a shift of
the origin without a change in orientation, then, the transformation is a
translation.
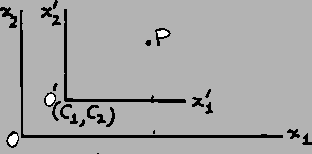
![]() has coordinates
has coordinates ![]() and
and
![]() with respect to
with respect to ![]() and
and
![]() respectively and
respectively and ![]() are the
coordinates of
are the
coordinates of ![]() with respect to
with respect to
![]() , then
, then
![]() are
obtained by rotating
are
obtained by rotating ![]() and
and ![]() through an angle
through an angle ![]() in the
counter-clockwise direction, then
in the
counter-clockwise direction, then
![]() have coordinates
have coordinates ![]() and
and
![]() relative
to
relative
to
![]() and
and
![]() respectively. Then,
respectively. Then,
![$\displaystyle \left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22}\end{ar...
...ray}{cc} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta\end{array}\right].$](img202.gif)
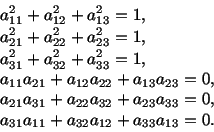
![]() and
and
![]() . By setting the volume of this
cube equal to 1, show that
. By setting the volume of this
cube equal to 1, show that
![]() .
.
![]() emanating from the origin
emanating from the origin ![]() and
ending at a point
and
ending at a point ![]() . With respect to the primed and unprimed axes,
. With respect to the primed and unprimed axes,
![]() with
respect to
unprimed axes are
with
respect to
unprimed axes are
![]() . Consider a set of primed
coordinate axes obtained by rotating the unprimed axes through an angle of
. Consider a set of primed
coordinate axes obtained by rotating the unprimed axes through an angle of
![]() about the
about the ![]() -axis (see Fig. ). What are the components,
-axis (see Fig. ). What are the components,
![]() , of this vector with respect to the primed set of axes?
, of this vector with respect to the primed set of axes?
![$\displaystyle [a_{ij}] = [\mathbf{e}^\prime_i\cdot \mathbf{e}_j] = \left[\begin...
...}\cos 30 & \sin 30 & 0\\ -\sin 30 & \cos 30 & 0\\ 0 & 0 & 1\end{array}\right]$](img282.gif)
![$\displaystyle \left[\begin{array}{c}A^\prime_1\\ A^\prime_2\\ A^\prime_3\end{...
...ray}\right] = \left[\begin{array}{c}\sin 30\\ \cos 30\\ 1\end{array}\right] .$](img284.gif)