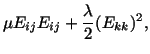(a) Substitution
If
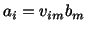 |
(2.6.1) |
and
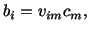 |
(2.6.2) |
then, in order to substitute for 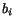 's from (2.6.2) into
(2.6.1) we first change
the dummy index from
's from (2.6.2) into
(2.6.1) we first change
the dummy index from 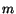 to some other letter, say
to some other letter, say 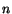 and then
the free index in (2.6.2) from
and then
the free index in (2.6.2) from 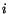 to
to 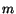 , so that
, so that
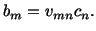 |
(2.6.3) |
Now (2.6.1) and (2.6.3) give
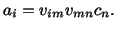 |
(2.6.4) |
Note that (2.6.4) represents three equations each having the
sum of nine terms on its right-hand side.
(b) Multiplication
It is important to note that
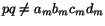 . In fact the
right-hand side of this expression is not even defined in the summation
convention and further it is obvious that
. In fact the
right-hand side of this expression is not even defined in the summation
convention and further it is obvious that
(c) Factoring
If
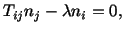 |
(2.6.8) |
then, using the Kronecker delta, we can write
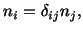 |
(2.6.9) |
so that (2.6.8) becomes
Thus
(d) Contraction
The operation of identifying two indices and so summing on them is known as
contraction. For example, 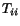 is the contraction of
is the contraction of 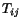 ,
,
and 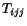 is a contraction of
is a contraction of 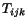 ,
,
If
then
Exercise. Given that
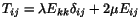 ,
,
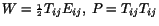 ,
show that
,
show that
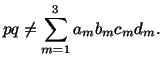
![]() is the contraction of
is the contraction of ![]() ,
,