Next: Manipulations with the Indicial Up: Mathematical Preliminaries Previous: Index Notation
The permutation symbol, denoted by
![]() , is defined by
, is defined by
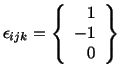 if if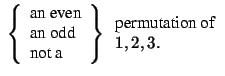 |
(2.5.1) |
| (2.5.2) |
| (2.5.3) |
Exercise. Using the index notation write an expression for
![]() ;
; ![]() being the angle between vectors
being the angle between vectors
![]() and
and
![]() .
.
Exercise. Show that
The following useful identity, which can be verified by long-hand calculations should be memorized.
| (2.5.4) |
![$\displaystyle {\rm det}\, \left[\begin{array}{ccc} A_{11} & A_{12} & A_{13}\\ A_{21} & A_{22} & A_{23}\\ A_{31} & A_{32} & A_{33}\end{array}\right],$](img136.gif) |
||
Example. Show that
![]() .
.