Next: Permutation Symbol Up: Mathematical Preliminaries Previous: Kronecker Delta.
Usually, rectangular Cartesian
coordinates of a point are denoted by ![]() and the unit vectors
along
and the unit vectors
along ![]() and
and ![]() -axes by
-axes by
![]() , and
, and
![]() respectively.
In this coordinate system, the components of a vector
respectively.
In this coordinate system, the components of a vector
![]() along
along ![]() , and
, and ![]() axes are denoted by
axes are denoted by ![]() , and
, and ![]() . The vector
. The vector
![]() has the representation
has the representation
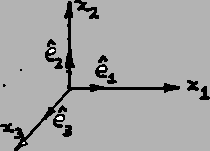
along ![]() and
and ![]() axes by
axes by
![]() ,
and
,
and
![]() respectively. Naturally then components of a vector
respectively. Naturally then components of a vector
![]() along
along ![]() and
and ![]() axes will be indicated by
axes will be indicated by ![]() , and
, and ![]() respectively. Hence we can write
respectively. Hence we can write
| (2.4.1) |
| (2.4.2) |
| (2.4.3) |
Exercise. Using the index notation, write expressions for
As another illustration of the use of the
index notation, consider a line element
with components
![]() . The square of the length,
. The square of the length, ![]() ,
of the line element is given by
,
of the line element is given by
Finally, we note that the differential of a function
![]() can be written as
can be written as
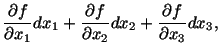 |
||
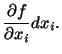 |