Let
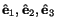 be a set of
orthonormal basis vectors (i.e.
be a set of
orthonormal basis vectors (i.e.
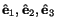 are mutually orthogonal
unit vectors). For any vector
are mutually orthogonal
unit vectors). For any vector
 ,
,
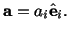 |
(2.8.3.1) |
Let
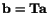 . Then
. Then
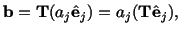 |
(2.8.3.2) |
or
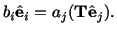 |
(2.8.3.3) |
Taking the inner product of both sides of this eqn. with
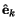 ,
we obtain
,
we obtain
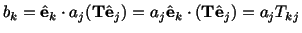 |
(2.8.3.4) |
where
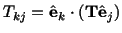 |
(2.8.3.5) |
is called the component of
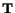 with respect to the
basis
with respect to the
basis
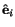 .
.
For computation purposes, eqn. (2.8.3.4) is written as
![$\displaystyle \left\{\begin{array}{c} b_1\\ b_2\\ b_3\end{array}\right\} = \l...
...\end{array}\right]\left\{\begin{array}{c} a_1\\ a_2\\ a_3\end{array}\right\}.$](img316.gif) |
(2.8.3.6) |
Analogous to the representation (2.8.3.1) for vector
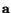 , we have
the following representation for second-order tensor
, we have
the following representation for second-order tensor
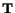 .
.
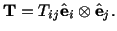 |
(2.8.3.7) |
Because of (2.8.2.2), 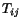 need not equal
need not equal 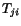 . In
order to see that (2.8.3.7) is equivalent to (2.8.3.5), we
evaluate
. In
order to see that (2.8.3.7) is equivalent to (2.8.3.5), we
evaluate
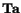 .
.
which is equivalent to
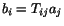 or (2.8.3.4).
or (2.8.3.4).
It is clear from (2.8.3.7) that the components 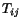 of
of
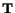 depend
upon the choice of basis
depend
upon the choice of basis
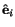 . Let
. Let
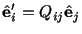 |
(2.8.3.9) |
where
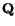 is an orthogonal matrix (i.e.
is an orthogonal matrix (i.e.
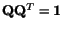 ).
Then
).
Then
Hence
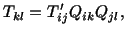 |
(2.8.3.11) |
and in matrix notation,
![$\displaystyle [T] = [Q]^T[T^\prime][Q],$](img333.gif) |
(2.8.3.12) |
and since
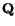 is orthogonal,
is orthogonal,
![$\displaystyle [T^\prime] = [Q][T][Q]^T.$](img334.gif) |
(2.8.3.13) |
The transpose
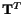 of a second-order tenseor
of a second-order tenseor
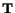 is defined
by
is defined
by
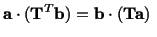 for every vector for every vector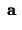 and and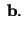 |
(2.8.3.14) |
The components of
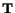 and
and
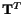 are related by
are related by
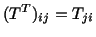 |
(2.8.3.15) |
![]() be a set of
orthonormal basis vectors (i.e.
be a set of
orthonormal basis vectors (i.e.
![]() are mutually orthogonal
unit vectors). For any vector
are mutually orthogonal
unit vectors). For any vector
![]() ,
,
![]() ,
we obtain
,
we obtain
![$\displaystyle \left\{\begin{array}{c} b_1\\ b_2\\ b_3\end{array}\right\} = \l...
...\end{array}\right]\left\{\begin{array}{c} a_1\\ a_2\\ a_3\end{array}\right\}.$](img316.gif)
![]() , we have
the following representation for second-order tensor
, we have
the following representation for second-order tensor
![]() .
.
![]() of
of
![]() depend
upon the choice of basis
depend
upon the choice of basis
![]() . Let
. Let
![]() of a second-order tenseor
of a second-order tenseor
![]() is defined
by
is defined
by