Description of Motion of a Continuum.

Let us suppose that a body, at time $t = t_0$, occupies a region of the physical space. The position of a particle at this time can be described by its coordinates $X_i$ with respect to a fixed rectangular Cartesian coordinate system.

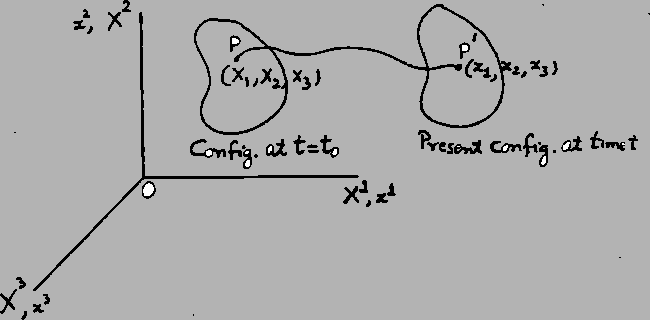
Let the body undergo a motion and point $P$ move to $P^\prime$ whose coordinates with respect to the same fixed axes are $x_i$. Then an equation of the form

$$x_i = x_i (X_1,\ X_2,\ X_3,\ t)$$ (3.1.1)

describes the path of the particle which at $t = t_0$ is located at $X_i$. In eqn. (3.1.1) the triplet $(X_1,\ X_2,\ X_3)$ serves to identify different particles of the body and is known as reference coordinates. The triplet $(x_1,\ x_2,\ x_3)$ gives the present position of the particle which at time $t = t_0$ was at the place $X_i$. Note that for a specific particle eqn. (3.1.1) defines the path line (or trajectory) of the particle. Of course

$$X_i = x_i (X_1,\ X_2,\ X_3,\ t_0),$$

which merely verifies the fact that the particle under consideration occupied the place $X_i$ at $t = t_0$.

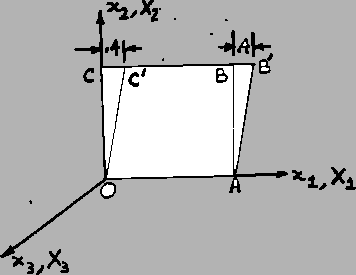
Example: Consider the motion

$$x_1 = X_1 + 0 \cdot 2tX_2,$$

$$x_2 = X_2,$$

$$x_3 = X_3,$$

where $(X_1,\ X_2,\ X_3)$ gives the position of a particle at $t = 0$. Sketch the configuration at time $t = 2$ for the body which at $t = 0$ has the shape of a cube of unit sides with one corner at the origin.

Solution: For the particle which at $t = 0$ was at the origin,

$$x_i = 0\ \ t.$$

Thus this particle stays at the origin at all times.

Similarly, the particle which at time $t = 0$ was at the position $(X_1,\ 0,\ 0)$ will move to $x_i = X_1\delta_{1i}$. That is, particles on line $OA$ do not move.

A particle $(X_1,\ 1,\ 0)$ on line $CB$ will occupy, at time $t = 2$, the position

$$x_i = (X_1 + 0 \cdot 2(2)\ (1))\delta_{1i} + (1)\delta_{2i}.$$

Thus every particle on line $CB$ is displaced horizontally to the right through a distance $(0\cdot 2)\ (2) = 0\cdot 4$.

A particle $(0,\ X_2,\ 0)$ on line $OC$ moves to

$$x_i = (0 + 0 \cdot 2(2)X_2)\delta_{1i} + X_2\delta_{2i}\ ,$$

so that every particle on the line $OC$ moves horizontally to the right through a distance linearly proportional to its height, that is, it remains a straight line. A similar situation prevails for the line $BA$.

Thus at time $t = 2$, the side view of the cube changes from a square to a parallelogram as shown.

The motion given in this example is known as simple shearing motion.