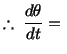When a continuum is in motion, quantities (such as temperature 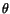 ,
velocity
,
velocity
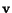 ) that are associated with specific particles change with
time. There are two ways to describe these changes.
) that are associated with specific particles change with
time. There are two ways to describe these changes.
- (i)
- Following the particles, that is, we express
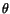 ,
, 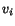 as functions of the coordinates of a particle in a fixed
reference configuration and time
as functions of the coordinates of a particle in a fixed
reference configuration and time 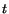 . Said differently, we express
. Said differently, we express
Such a description is
known as Lagrangian or referential or
material description.
- (ii)
- Observing the changes at fixed locations, that is, we express
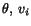 etc. as functions of
etc. as functions of 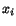 and
and 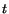 . Thus
. Thus
Such a description is known as spatial or Eulerian.
We note that in this description, what is described (or
measured) is the change of quantities at a fixed point in space (not a
specific material particle) as a function of time. The same
spatial position is
occupied by different particles at different times. Therefore, the spatial
description does not provide direct information regarding the
changes in the values of a quantity associated with a material particle as it
moves about in space.
The referential and spatial descriptions are, of course, related by the
motion. That is, if the motion is known then, one description can be obtained
from the other as illustrated by the following example.
Example: Given the motion of a body to be
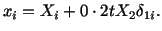 |
(i) |
For the temperature field given by
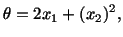 |
(ii) |
- (a)
- find the material description of temperature, and
- (b)
- the rate
of change of temperature of a particle which at time
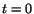 was at the place
was at the place
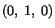 .
.
Solution
- (a)
- By substituting (i) into (ii), we obtain
- (b)
- The temperature of the desired particle at different
times is given by
Note that even though the temperature is independent of time in the spatial
description, a particle experiences a change in temperature as it moves
from one spatial position to another; this becomes clear from eqn. (iii).
Whereas spatial description is often used in fluid mechanics, referential
description is employed
in solid mechanics and in formulating laws of mechanics.
![]() ,
velocity
,
velocity
![]() ) that are associated with specific particles change with
time. There are two ways to describe these changes.
) that are associated with specific particles change with
time. There are two ways to describe these changes.