Next: Restrictions on Continuous Deformation Up: Kinematics Previous: Referential and Spatial Descriptions
By definition, the displacement vector ![]() of a particle is the
difference between its
position vectors at time
of a particle is the
difference between its
position vectors at time ![]() and at time
and at time ![]() (or 0).
(or 0).
| (3.3.1) |
| (3.3.2) | ||
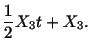 |
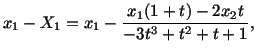 |
||
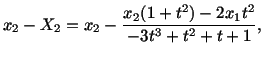 |
||
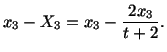 |