For 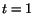 , eqns. (3.3.2) give
, eqns. (3.3.2) give
Thus points
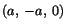 in the reference configuration move to
in the reference configuration move to
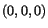 at time
at time 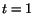 . This implies that distinct particles which occupy
different places in the reference configuration are deformed into
the same place in the
present configuration (at time
. This implies that distinct particles which occupy
different places in the reference configuration are deformed into
the same place in the
present configuration (at time 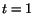 ). This amounts to the
collision of various
material particles. Even though in particle mechanics collisions are
allowed, in continuum mechanics, such a possibility is assumed to be ruled out
to start with. Thus in continuum mechanics it is assumed that different
material particles always occupy distinct places. This is equivalent to the
requirement that
). This amounts to the
collision of various
material particles. Even though in particle mechanics collisions are
allowed, in continuum mechanics, such a possibility is assumed to be ruled out
to start with. Thus in continuum mechanics it is assumed that different
material particles always occupy distinct places. This is equivalent to the
requirement that
be a one-to-one mapping of 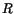 onto the present configuration.
Since in Continuum Mechanics we will need to differentiate functions with
respect to
onto the present configuration.
Since in Continuum Mechanics we will need to differentiate functions with
respect to 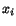 or
or 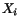 , we will henceforth assume that the mapping
, we will henceforth assume that the mapping
is continuously differentiable and has a continuously
differentiable inverse given by
This is so if and only if the Jacobian 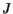 defined by
defined by
![\begin{equation*}J = {\rm det}\left[\begin{array}{ccc}\displaystyle\frac{\partia...
... \displaystyle\frac{\partial x_3}{\partial X_3}\end{array}\right]\end{equation*}](img418.gif) |
(3.4.1) |
is non-zero for all points in 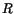 and for every
value of
and for every
value of 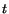 . Since
. Since
and 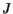 is a continuous function of
is a continuous function of 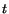 , therefore,
, therefore, 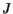 must be
positive for every
must be
positive for every 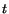 . Using the index notation, we can write
. Using the index notation, we can write 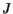 as
as
![$\displaystyle J = {\rm det}\left[\frac{\partial x_i}{\partial X_j}\right] = {\rm det}\left[\delta_{ij} + \frac{\partial u_i}{\partial X_j}\right].$](img420.gif) |
(3.4.2) |
In summary, we can conclude from the preceding discussion that
a necessary and sufficient condition for a continuous deformation to be
physically admissible is that the Jacobian 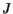 be greater than zero.
be greater than zero.
A displacement field satisfying the condition 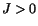 is said to be proper and admissible, or
simply admissible.
is said to be proper and admissible, or
simply admissible.
Thus, for an admissible deformation of a medium the displacement components
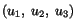 must satisfy
must satisfy 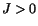 . For example, a
piece of rubber can not be subjected
to displacement components
. For example, a
piece of rubber can not be subjected
to displacement components
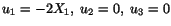 since then
since then 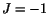 . This displacement is called a reflection about
the
. This displacement is called a reflection about
the
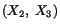 plane, since the point
plane, since the point
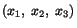 is the image of the point
is the image of the point
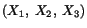 in a mirror that lies
in the plane
in a mirror that lies
in the plane 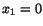 .
.
Exercise: Determine whether or not
where 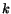 is a constant, are possible displacement
components for a continuous medium.
is a constant, are possible displacement
components for a continuous medium.
![]() , eqns. (3.3.2) give
, eqns. (3.3.2) give
![\begin{equation*}J = {\rm det}\left[\begin{array}{ccc}\displaystyle\frac{\partia...
... \displaystyle\frac{\partial x_3}{\partial X_3}\end{array}\right]\end{equation*}](img418.gif)
![$\displaystyle J = {\rm det}\left[\frac{\partial x_i}{\partial X_j}\right] = {\rm det}\left[\delta_{ij} + \frac{\partial u_i}{\partial X_j}\right].$](img420.gif)
![]() is said to be proper and admissible, or
simply admissible.
is said to be proper and admissible, or
simply admissible.
![]() must satisfy
must satisfy ![]() . For example, a
piece of rubber can not be subjected
to displacement components
. For example, a
piece of rubber can not be subjected
to displacement components
![]() since then
since then ![]() . This displacement is called a reflection about
the
. This displacement is called a reflection about
the
![]() plane, since the point
plane, since the point
![]() is the image of the point
is the image of the point
![]() in a mirror that lies
in the plane
in a mirror that lies
in the plane ![]() .
.