Next: Boundary Conditions for the Up: The Stress Tensor Previous: The Stress Tensor
In this section we will study the laws of motion applicable to a continuous medium similar to Newton's laws of motion studied in particle mechanics. We first review Newton's laws of motion below.
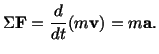 |
(4.1.1) |
Newton's first law of motion defines an inertial frame. That is, an inertial frame is one in which Newton's first law of motion holds. Usually, it is taken as a frame attached to the Sun. However, in most engineering problems, one can take the co-ordinate axes fixed to the earth as an inertial frame without introducing any appreciable error. Hereafter, we will take an inertial frame as the frame of reference.
To write the laws of motion for a continuum we note that the linear momentum
of the material enclosed in an infinitesimal volume ![]() is
is
![]() where
where ![]() is the mass density and
is the mass density and
![]() is the
velocity. Hence the linear momentum of the shaded portion is
is the
velocity. Hence the linear momentum of the shaded portion is
![]() in which the integration is over the shaded region. To find
the resultant force acting on this region of interest, we observe that we have
two kinds of forces.
in which the integration is over the shaded region. To find
the resultant force acting on this region of interest, we observe that we have
two kinds of forces.
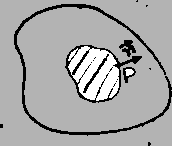
Body forces are forces that act on all particles in a body as a
result of some external body or effect not in direct contact with the body
under consideration. An example of this is the gravitational force exerted on
a body. This type of force is defined as a force intensity per unit mass or
per unit volume at a point in the continuum. Thus, if the body
force per unit mass is ![]() , then the body force on the material enclosed in
the shaded region will be
, then the body force on the material enclosed in
the shaded region will be ![]() .
.
Surface forces are contact forces that act across a surface of the
body, which may be internal or external. In non-polar continuum mechanics we
assume that the action of that part of the body which is exterior to the
shaded region on the body enclosed in the shaded region is equipollent to a
system of forces acting on the bounding surface of the shaded region. The
assumption that the contact force is of this kind is the cut principle
of Cauchy: Within the shape of a body at any given time, conceive a smooth,
closed diaphragm; then the action of the part of the body outside that
diaphragm and adjacent to it on that inside is equipollent to that of a field
of vectors defined on the diaphragm. Note that no point moments are assumed
to be exerted by one part of the body on its adjacent part across the common
surface. Thus in nonpolar continuum mechanics, moments are caused by the
forces. The contact force at a point ![]() on a surface is usually given as a
force
on a surface is usually given as a
force
![]() acting on a unit area surrounding
acting on a unit area surrounding ![]() and lying on the
surface. Through a given point in the body, there are infinitely many
surfaces. The intensity of the contact force at the point
and lying on the
surface. Through a given point in the body, there are infinitely many
surfaces. The intensity of the contact force at the point ![]() on each of
these surfaces will, in general, be different. How does
on each of
these surfaces will, in general, be different. How does
![]() at the
point
at the
point ![]() depend upon the surface through
depend upon the surface through ![]() ? In the classical continuum
mechanics, it is assumed that the intensity of the contact force on all
surfaces with a common tangent plane at
? In the classical continuum
mechanics, it is assumed that the intensity of the contact force on all
surfaces with a common tangent plane at ![]() is the same. That
is,
is the same. That
is,
![]() at
at ![]() is assumed to depend upon the surface through
is assumed to depend upon the surface through ![]() only
through the oriented normal
only
through the oriented normal
![]() of the surface at
of the surface at ![]() .
.
| (4.1.2) |
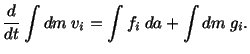 |
(4.1.3) |
Equation (4.1.3) is known as the conservation of linear momentum. A similar equation
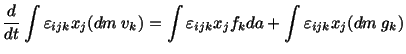 |
(4.1.4) |
Since
![]() , therefore, equations (4.1.3) and (4.1.4) can
also be written as
, therefore, equations (4.1.3) and (4.1.4) can
also be written as
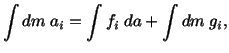 |
(4.1.5) | |
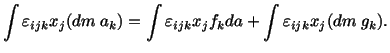 |
(4.1.6) |
We now study the dependence of
![]() upon
upon
![]() in some detail.
Consider a cylinder of radius
in some detail.
Consider a cylinder of radius ![]() and height
and height
![]() with the top and
bottom faces perpendicular to
with the top and
bottom faces perpendicular to
![]() and the point
and the point ![]() lying on one of
the end faces. We apply
the balance of linear momentum (4.1.5) to the material
lying on one of
the end faces. We apply
the balance of linear momentum (4.1.5) to the material
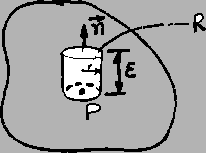
contained within this cylinder. Using the mean-value theorem of calculus, we obtain
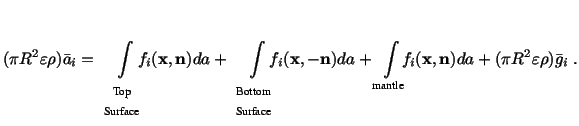 |
(4.1.7) |
![$\displaystyle 0 = \int [f_i (\mathbf{x},\mathbf{n}) + f_i(\mathbf{x},-\mathbf{n})]da.$](img1165.gif) |
| (4.1.8) |
This is known as Cauchy's Fundamental Lemma and states that
![]() is an odd function of
is an odd function of
![]() . We now show that
. We now show that
![]() is in fact linear in
is in fact linear in
![]() . Consider a tetrahedron, three
sides of which are mutually orthogonal, the fourth having outward unit normal
. Consider a tetrahedron, three
sides of which are mutually orthogonal, the fourth having outward unit normal
![]() .
.
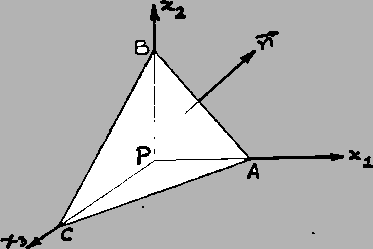
Let the area of the inclined plane ![]() be
be ![]() . Then the areas of
planes
. Then the areas of
planes ![]() ,
, ![]() and
and ![]() are
are ![]() ,
, ![]() and
and ![]() respectively. On
applying eqn. (4.1.5) to the material contained in the tetrahedron, and using
the mean-value theorem, we obtain
respectively. On
applying eqn. (4.1.5) to the material contained in the tetrahedron, and using
the mean-value theorem, we obtain
| (4.1.9) |
| (4.1.10) |
| (4.1.11) |
| (4.1.12) |
By comparing the right-hand sides of (4.1.10) and (4.1.12) we get
| (4.1.13) |
From equation (4.1.13) it is clear that stress vectors on three mutually
perpendicular planes at a point determine the stress tensor at that point.
Because of eqn. (4.1.12) or (4.1.10), stress vectors on three mutually
perpendicular planes at a point also determine the stress vector on any other
plane. This proves Cauchy's fundamental theorem: From the stress
vectors acting on three mutually perpendicular planes at a point,
stress vectors on every plane through
the point can be determined; they are given by (4.1.12) as
linear functions of the stress tensor ![]() .
.
A glance at equations (4.1.5) and (4.1.6) reveals that one integration in each equation is over the surface area whereas others are over the region under consideration. We now transform this surface integral into the volume integral by using the divergence theorem. Note that
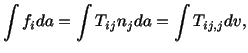 |
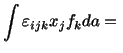 |
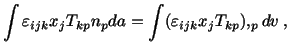 |
|
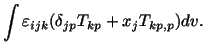 |
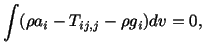 |
![$\displaystyle \int \varepsilon_{ijk}[x_j(\rho a_k - T_{kp,p} - \rho g_k) - T_{kj}]dv = 0.$](img1198.gif) |
| (4.1.14) | ||
| (4.1.15) |
For static problems ![]() and eqn. (4.1.14) gives
and eqn. (4.1.14) gives
| (4.1.16) |
Example: Show that the following stress field
Solution
Exercise: Suppose that the body force is
![]() , where
, where ![]() is a constant. Consider the following stress
tensor
is a constant. Consider the following stress
tensor
![$\displaystyle [\textbf{T}] = \alpha \left[\begin{array}{ccc} x_2 & -x_3 & 0\\ -x_3 & 0 & -x_2\\ 0 & -x_2 & T_{33}\end{array}\right]\ .$](img1215.gif) |
Exercise: Suppose that the stress distribution has the form (called plane stress)
![$\displaystyle [T_{ij}] = \left[\begin{array}{ccc} T_{11} (x_1,x_2) & T_{12} (x_...
... 0\\ T_{12} (x_1,x_2) & T_{22} (x_1,x_2) & 0\\ 0 & 0 & 0\end{array}\right]\ .$](img1217.gif) |