Boundary Conditions for the Stress Tensor

Applied distributed forces on the surface of a body are called surface tractions. We wish to find the relation between the surface tractions and the stress field defined within the body. This relation is eqn. (4.1.12) in which the left-hand side represents the surface tractions applied to the bounding surface of the body. The equation

$$T_{ij} (\mathbf{x})n_j = f_i (\mathbf{x})$$

for points $\mathbf{x}$ on the bounding surface of the body is called the boundary condition.

Example: A long prismatic dam is subjected to water pressure that increases linearly with the depth. The dam has thickness $2b$ and height $h$. Write the traction boundary conditions for the traction-type bounding surfaces of the dam.

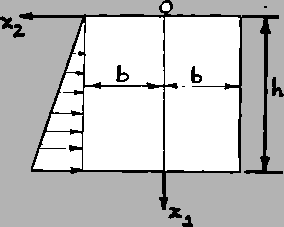
Solution: At the top surface $\mathbf{n} = (-1,0,0)$. Since there is no applied force on this surface, therefore

$$T_{ij}n_j = -T_{i1} = 0\ \ \ x_1 = 0.$$

On the plane $x_2 = -b,\ \mathbf{n} = (0,-1,0)$. There is no force applied on this surface, therefore,

$$T_{ij}n_j = -T_{i2} = 0\ \ \ x_2 = -b.$$

On the plane $x_2 = b,\ \mathbf{n} = (0,1,0)$. The water pressure at any point on this plane exerts a normal force equal to $-\rho_wgx_1\mathbf{e}_2$ in which $\rho_w$ is the mass density of water, $g$ is the gravitational constant. Therefore,

$$T_{ij}n_j = T_{i2} = -\rho_wgx_1\delta_{i2}\ \ \ x_2 = b.$$

The lower surface of the dam is in contact with the ground and the boundary conditions on it depend upon whether the ground is taken as deformable or rigid; we will not discuss these boundary conditions here.

Example: Write the traction boundary conditions at the inner and the outer surfaces of a cylindrical pressure vessel subjected to an internal pressure $p_1$ and external pressure $p_2$.

Solution: At a point on the inner surface $\mathbf{n} = \left( - \frac{x_1}{a},\ -\frac{x_2}{a},0\right)$. Therefore,

$$T_{ij}n_j = f_i = -p_1n_i$$

simplifies to

$$T_{11} x_1 + T_{12} x_2 = -p_1x_1,$$

$$T_{21}x_1 + T_{22} x_2 = -p_1x_2,$$

$$T_{31}x_1 + T_{32}x_2 = 0.$$

At a point on the outer surface $\mathbf{n} = \left(\frac{x_1}{b},\frac{x_2}{b},0\right)$. Therefore, the traction boundary condition on the outer surface are

$$T_{11}x_1 + T_{12}x_2 = -p_2x_1,$$

$$T_{21}x_1 + T_{22}x_2 = -p_2x_2,$$

$$T_{31}x_1 + T_{32}x_2 = 0.$$

Exercise: Given the following stress distribution

$$[\mathbf{T}] = \left[\begin{array}{ccc}x_1 + x_2 & T_{12}(x_1,x_2... ... T_{12}(x_1,x_2) & x_1 - 2x_2 & 0\\ 0 & 0 & x_2\end{array}\right]\times 10^3,$$

find $T_{12}$ in order that the stress distribution is in equilibrium with zero body force, and that the stress vector on the plane $x_1 = 1$ is given by $[(1 + x_2)\mathbf{e}_1 + (5 - x_2)\mathbf{e}_2]10^3$.

Exercise: Consider the following stress distribution for a certain circular cylindrical bar

$$[T] = \left[\begin{array}{ccc} 0 & -\alpha x_3 & \alpha x_2\\ -\alpha x_3 & 0 & 0\\ \alpha x_2 & 0 & 0\end{array}\right]\ ,$$

where $\alpha$ is a constant.

(a)

What is the distribution of the stress vector on the surfaces defined by $x^2_2 + x^2_3 = 4,\ x_1 = 0$, and $x_1 = \ell$?

 $&bull#bullet;$

Find the total resultant force and moment on the end face $x_1 = \ell$.