Solid mechanics problems are easy to formulate in the referential description.
However the balance laws (4.1.14) and (4.1.15) derived earlier are in
the spatial description. We note that the stress-vector
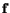 in
equations (4.1.5) and (4.1.6) is acting on a unit area in the present
configuration of the body. If we can express this
in
equations (4.1.5) and (4.1.6) is acting on a unit area in the present
configuration of the body. If we can express this
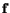 in terms of
the area in the reference configuration, we would then be able to write the
balance laws in the referential description. Note that
in terms of
the area in the reference configuration, we would then be able to write the
balance laws in the referential description. Note that
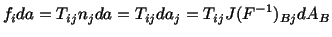 |
(4.3.1) |
where we have substituted for 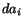 in terms of
in terms of 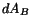 from
eqn. (3.10.1). With the following definition
from
eqn. (3.10.1). With the following definition
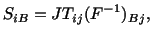 |
(4.3.2) |
equation (4.3.1) becomes
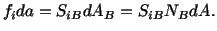 |
(4.3.3) |
Thus 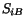 provides a measure of the present force acting on
a unit area in the reference configuration. For this reason,
provides a measure of the present force acting on
a unit area in the reference configuration. For this reason, 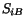 is
called the nominal stress tensor, engineering stress tensor, or
first Piola-Kirchhoff stress tensor. Note that
is
called the nominal stress tensor, engineering stress tensor, or
first Piola-Kirchhoff stress tensor. Note that
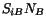 equals the present
equals the present
value of the force acting on the area
in the present configuration at 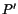 into which a unit area
perpendicular to
into which a unit area
perpendicular to
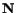 at
at  is deformed.
is deformed.
The stress tensors 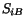 and
and 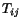 are related by eqn. (4.3.2).
However, to find one stress tensor from the other, one must know the
deformation gradient. In the Mechanics of Materials course,
the nominal stress tensor
are related by eqn. (4.3.2).
However, to find one stress tensor from the other, one must know the
deformation gradient. In the Mechanics of Materials course,
the nominal stress tensor 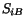 and the engineering strain
and the engineering strain 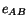 are used to
plot the stress strain curve. In general, the graph of the true stress
are used to
plot the stress strain curve. In general, the graph of the true stress
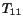 versus the true strain
versus the true strain
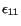 will look quite different
from that of
will look quite different
from that of 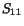 versus
versus 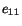 in a simple tension test in which the
load is applied in the
in a simple tension test in which the
load is applied in the 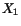 -direction, and
-direction, and 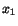 and
and 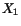 axes point in the
same direction.
axes point in the
same direction.
Substituting for 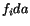 from (4.3.3) into (4.1.5) and writing
from (4.3.3) into (4.1.5) and writing
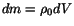 , we obtain
, we obtain
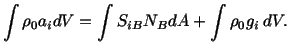 |
(4.3.4) |
Now using the divergence theorem, we convert the surface
integral on the right-hand side of (4.3.4) into the volume integral and
thereby obtain
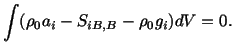 |
(4.3.5) |
This equation is to hold for all infinitesimal volume elements
in the body. If the integrand is continuous which is assumed to be
the case, then
(4.3.5) can hold for every volume element in the body if and only if
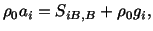 |
(4.3.6) |
or
This is Cauchy's first law of motion in the referential description.
From (4.1.15) and (4.3.2) we obtain the following for the second law of
motion.
![$\displaystyle [\mathbf{S}][\mathbf{F}]^T = [\mathbf{F}][\mathbf{S}]^T.$](img1270.gif) |
(4.3.7) |
Thus the nominal stress tensor 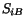 need not be and, in
general, is not symmetric.
need not be and, in
general, is not symmetric.
The traction type boundary conditions in terms of 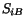 are written as
are written as
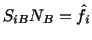 |
(4.3.8) |
in which 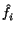 is the force acting at points on the
boundary in the deformed configuration but is measured per unit area in the
reference configuration.
is the force acting at points on the
boundary in the deformed configuration but is measured per unit area in the
reference configuration.
The following stress tensor is introduced in the engineering literature:
or
![$\displaystyle [\tilde{\mathbf{S}}] = J[\mathbf{F}^{-1}][\mathbf{T}][\mathbf{F}^{-1}]^T = [\mathbf{F}^{-1}][\mathbf{S}].$](img1274.gif) |
(4.3.9) |
The tensor
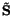 known as the
second Piola-Kirchhoff stress tensor is symmetric; the symmetry of
known as the
second Piola-Kirchhoff stress tensor is symmetric; the symmetry of
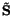 is equivalent to the Cauchy's second law of motion.
There is no easy physical interpretation of
is equivalent to the Cauchy's second law of motion.
There is no easy physical interpretation of
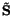 .
.
![]() in
equations (4.1.5) and (4.1.6) is acting on a unit area in the present
configuration of the body. If we can express this
in
equations (4.1.5) and (4.1.6) is acting on a unit area in the present
configuration of the body. If we can express this
![]() in terms of
the area in the reference configuration, we would then be able to write the
balance laws in the referential description. Note that
in terms of
the area in the reference configuration, we would then be able to write the
balance laws in the referential description. Note that
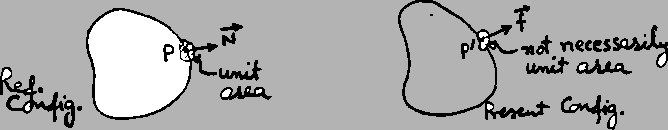
![]() into which a unit area
perpendicular to
into which a unit area
perpendicular to
![]() at
at ![]() is deformed.
is deformed.
![]() and
and ![]() are related by eqn. (4.3.2).
However, to find one stress tensor from the other, one must know the
deformation gradient. In the Mechanics of Materials course,
the nominal stress tensor
are related by eqn. (4.3.2).
However, to find one stress tensor from the other, one must know the
deformation gradient. In the Mechanics of Materials course,
the nominal stress tensor ![]() and the engineering strain
and the engineering strain ![]() are used to
plot the stress strain curve. In general, the graph of the true stress
are used to
plot the stress strain curve. In general, the graph of the true stress
![]() versus the true strain
versus the true strain
![]() will look quite different
from that of
will look quite different
from that of ![]() versus
versus ![]() in a simple tension test in which the
load is applied in the
in a simple tension test in which the
load is applied in the ![]() -direction, and
-direction, and ![]() and
and ![]() axes point in the
same direction.
axes point in the
same direction.
![]() from (4.3.3) into (4.1.5) and writing
from (4.3.3) into (4.1.5) and writing
![]() , we obtain
, we obtain
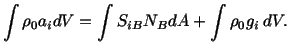
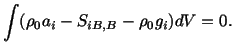
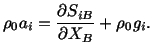
![]() are written as
are written as