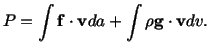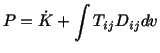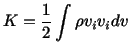Let us consider two sets of co-ordinate axes 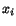 and
and
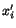 related by eqn. (2.7.4), that is,
related by eqn. (2.7.4), that is,
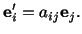 |
(2.7.4) |
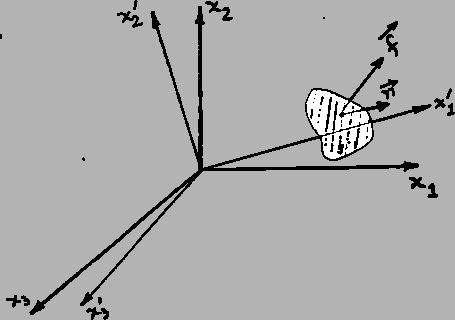
Consider a plane the outer normal to which points in the
positive
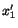 direction. Therefore, a unit normal
direction. Therefore, a unit normal
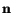 to
this plane can be written as
to
this plane can be written as
 |
(4.4.1) |
or
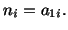 |
(4.4.2) |
The stress vector
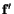 on this plane is given by
on this plane is given by
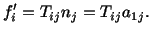 |
(4.4.3) |
Recalling the interpretations of various components
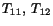 etc. of the stress tensor given after eqn. (4.1.3), we note that
etc. of the stress tensor given after eqn. (4.1.3), we note that
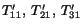 equal respectively, the
components of
equal respectively, the
components of
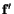 in the positive
in the positive
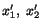 ,
and
,
and
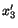 directions. Thus
directions. Thus
These three equations can be written as
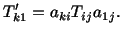 |
(4.4.5) |
Similarly, now consider planes whose outer normals point in the positive
 directions and proceed the way it was done to
arrive at (4.4.5). The result is
directions and proceed the way it was done to
arrive at (4.4.5). The result is
| |
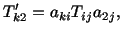 |
(4.4.6) |
| |
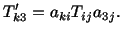 |
(4.4.7) |
Equations (4.4.5), (4.4.6) and (4.4.7) can be collectively written as
![$\displaystyle T^\prime_{kp} = a_{ki}T_{ij}a_{pj};\ [\mathbf{T}^\prime] = [\mathbf{a}][\mathbf{T}][\mathbf{a}]^T.$](img1293.gif) |
(4.4.8) |
A comparison of this equation with eqn. (2.8.4) reveals
that
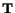 is indeed a second order tensor.
is indeed a second order tensor.
An application of eqn. (4.4.8) is the problem of finding the normal and the
shear stress on an oblique plane when the stress-state on horizontal and
vertical planes in the plane-stress problem is known.
For the axes shown,
Therefore
Thus one can find
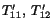 , the normal and
shear stresses on the oblique plane. Equations relating
, the normal and
shear stresses on the oblique plane. Equations relating
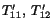 to
to
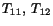 are called ``stress transformation
equations'' in the Mechanics of Deformable Bodies course.
are called ``stress transformation
equations'' in the Mechanics of Deformable Bodies course.
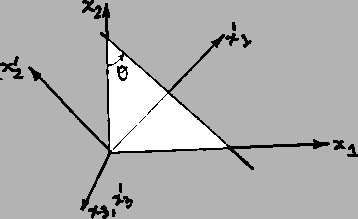
Exercise: The stress matrix
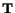 referred to
referred to
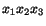 -axes is shown below at the left (in ksi). New
-axes is shown below at the left (in ksi). New
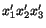 -axes are chosen by rotating the unprimed
axes as shown
to the right.
-axes are chosen by rotating the unprimed
axes as shown
to the right.
- a)
- Determine the traction vectors on each of the new
coordinate
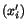 planes in terms of components referred to the old
planes in terms of components referred to the old
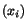 axes. For example, determine
axes. For example, determine
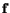 on the
on the
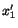 plane
in the form
plane
in the form
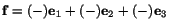 .
.
- (b)
- Now project each of the vectors obtained in (a) onto the three new
coordinate axes, and verify that the nine new components thus obtained for the
stress matrix
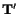 are the same as those given by the
formulae for the
transformation of a second-order tensor under the rotation of axes.
are the same as those given by the
formulae for the
transformation of a second-order tensor under the rotation of axes.
Exercise: The work 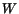 done by external forces during the
deformation of a continuous body is given by
done by external forces during the
deformation of a continuous body is given by
By substituting for
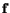 from eqn. (4.1.12), using the
divergence theorem and assuming that the body is deformed quasi-statically
(that is, the inertia force
from eqn. (4.1.12), using the
divergence theorem and assuming that the body is deformed quasi-statically
(that is, the inertia force 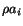 is negligible), show that
is negligible), show that
Hence show that for small deformations
Exercise: The power  of external forces is defined as
of external forces is defined as
By substituting for
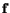 from eqn. (4.1.12), using the
divergence theorem and Cauchy's first law of motion, show that
from eqn. (4.1.12), using the
divergence theorem and Cauchy's first law of motion, show that
where
is the kinetic energy of the body.
![]() and
and
![]() related by eqn. (2.7.4), that is,
related by eqn. (2.7.4), that is,
![]() on this plane is given by
on this plane is given by
![]() directions and proceed the way it was done to
arrive at (4.4.5). The result is
directions and proceed the way it was done to
arrive at (4.4.5). The result is
![$\displaystyle [\mathbf{a}] = \left[\begin{array}{ccc} \cos\theta & \sin\theta & 0\\ -\sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{array}\right].$](img1295.gif)
![$\displaystyle \left[\begin{array}{ccc}T^\prime_{11} & T^\prime_{12} & T^\prime_...
...& -\sin\theta & 0\\ \sin\theta & \cos \theta & 0 \\ 0 & 0 & 1\end{array}\right]$](img1296.gif)
![$\displaystyle = \left[\begin{array}{ccc}T_{11}\cos^2\theta + T_{22}\sin^2 \thet...
...22}\cos^2\theta - 2T_{12}\sin\theta\cos\theta & 0\\ 0 & 0 & 0\end{array}\right]$](img1298.gif)
![]() referred to
referred to
![]() -axes is shown below at the left (in ksi). New
-axes is shown below at the left (in ksi). New
![]() -axes are chosen by rotating the unprimed
axes as shown
to the right.
-axes are chosen by rotating the unprimed
axes as shown
to the right.
![\begin{equation*}[\mathbf{T}]= \left[\begin{array}{ccc} 50 & 37.5 & 0\\ 37.5 & ...
...-.1in} \multicolumn{4}{l}{\underline{\hspace{1.5in}}} \end{array}\end{equation*}](img1302.gif)
![]() done by external forces during the
deformation of a continuous body is given by
done by external forces during the
deformation of a continuous body is given by
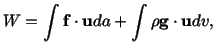
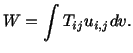
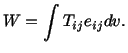
![]() of external forces is defined as
of external forces is defined as