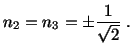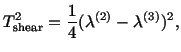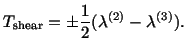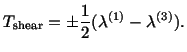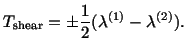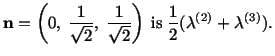In stress analysis problems one is interested in finding the maximum and the
minimum normal stress and the maximum shearing stress at a point. In the
following discussion, the point
 in the present configuration
is kept fixed.
in the present configuration
is kept fixed.
At a point
 in the present configuration of the body, consider a plane whose
outer unit
normal is
in the present configuration of the body, consider a plane whose
outer unit
normal is
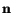 . The stress vector
. The stress vector
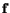 on this plane
given by equation (4.1.12) is
on this plane
given by equation (4.1.12) is  . The normal stress on this plane is
given by
. The normal stress on this plane is
given by
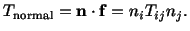 |
(4.5.1) |
Thus the problem of finding the maximum or the minimum normal
stress at the point
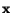 reduces
to finding the unit vector
reduces
to finding the unit vector
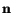 for
which
for
which
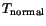 is maximum or minimum. Using the method of Lagrange
multiplier, the problem becomes that of finding extreme values of the
function
is maximum or minimum. Using the method of Lagrange
multiplier, the problem becomes that of finding extreme values of the
function
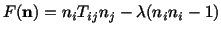 |
(4.5.2) |
in which 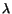 is an arbitrary scalar. The vector
is an arbitrary scalar. The vector
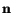 which makes
which makes 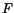 assume a maximum or minimum value is given by
assume a maximum or minimum value is given by
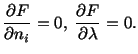 |
(4.5.3) |
That is
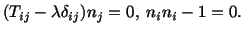 |
(4.5.4) |
A nontrivial solution of eqn. (4.5.4)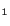 exists if and only if
exists if and only if
![$\displaystyle {\rm det}\ [T_{ij} - \lambda\delta_{ij}] = 0$](img1322.gif) |
(4.5.5) |
which gives the cubic equation
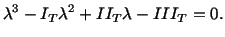 |
(4.5.6) |
Here
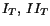 and
and 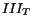 are the principal invariants of
are the principal invariants of
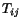 . Since
. Since 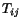 is symmetric, therefore, eqn. (4.5.6) has three real
eigenvalues
is symmetric, therefore, eqn. (4.5.6) has three real
eigenvalues
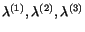 . Corresponding to
each of these eigenvalues we can find a unit vector
. Corresponding to
each of these eigenvalues we can find a unit vector
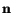 from eqn. (4.5.4). For example,
from eqn. (4.5.4). For example,
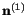 corresponding to
corresponding to
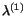 is
given by
is
given by
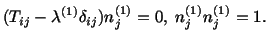 |
(4.5.7) |
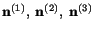 are
normals to planes on which
are
normals to planes on which
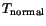 assumes extreme values. Since
assumes extreme values. Since
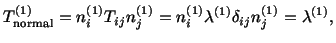 |
(4.5.8) |
therefore
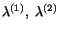 and
and
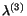 are extreme values of normal stresses. Also the stress vector on the plane
with outer unit normal
are extreme values of normal stresses. Also the stress vector on the plane
with outer unit normal
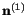 is given by
is given by
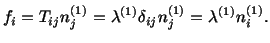 |
(4.5.9) |
Let
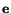 a unit vector in this plane. Then the shear
stress in the direction of
a unit vector in this plane. Then the shear
stress in the direction of
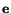 on the
on the
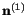 plane is given by
plane is given by
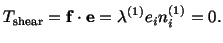 |
(4.5.10) |
The plane on which the shear stress is zero is called a
principal plane and the normal stress on a principal plane is called a
principal stress. Thus
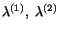 and
and
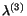 are principal stresses and
are principal stresses and
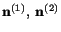 and
and
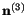 are normals to principal planes.
are normals to principal planes.
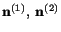 and
and
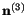 are called principal axes
of the stress.
are called principal axes
of the stress.
Whenever
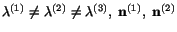 and
and
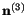 are uniquely determined and are
mutually orthogonal. However, when any two or all three of the principal
stresses are equal, then
are uniquely determined and are
mutually orthogonal. However, when any two or all three of the principal
stresses are equal, then
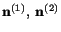 and
and
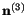 are not uniquely determined but can still be found so that
they are mutually orthogonal. Henceforth, in this section, we
will assume that the principal axes of the stress tensor are mutually
orthogonal.
are not uniquely determined but can still be found so that
they are mutually orthogonal. Henceforth, in this section, we
will assume that the principal axes of the stress tensor are mutually
orthogonal.
Taking
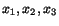 axes along the principal axes of the stress, we see
that with respect to these axes
axes along the principal axes of the stress, we see
that with respect to these axes 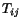 has the form
has the form
![$\displaystyle [T_{ij}] = \left[\begin{array}{ccc} \lambda^{(1)} & 0 & 0\\ 0 & \lambda^{(2)} & 0\\ 0 & 0 & \lambda^{(3)}\end{array}\right].$](img1339.gif) |
(4.5.11) |
We now find the plane of the maximum shear stress. Let an outer unit
normal to this
plane be
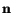 . Then, taking principal axes of stress as the
coordinate axes,
. Then, taking principal axes of stress as the
coordinate axes,
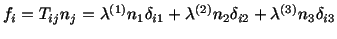 |
(4.5.12) |
gives the traction on this plane. Therefore the shear stress on
this plane is given by
Thus the problem of determining maximum
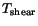 reduces to
that of finding extreme values of the function
reduces to
that of finding extreme values of the function
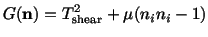 |
(4.5.14) |
in which 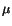 is a Lagrange multiplier. The necessary conditions are
is a Lagrange multiplier. The necessary conditions are
which are equivalent to
| |
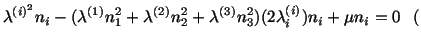 no summation on no summation on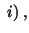 |
(4.5.15) |
| |
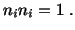 |
(4.5.16) |
Three equations given by (4.5.15) for 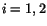 and
and 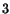 and the eqn. (4.5.16)
determine
and the eqn. (4.5.16)
determine 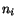 and
and 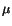 . A solution of these equations for which two out of
. A solution of these equations for which two out of
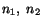 and
and 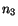 are zero is not interesting since this corresponds to
finding
are zero is not interesting since this corresponds to
finding
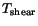 on a principal plane which is zero. The
solution of (4.5.15) and (4.5.16) for which
on a principal plane which is zero. The
solution of (4.5.15) and (4.5.16) for which
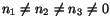 exists
only if
exists
only if
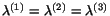 . In this case too,
eqn. (4.5.13) gives
. In this case too,
eqn. (4.5.13) gives
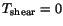 .
.
The remaining possibility is that one out of 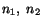 and
and 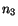 be
zero, say
be
zero, say
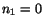 ,
,
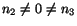 . For this case, eqn. (4.5.15) for
. For this case, eqn. (4.5.15) for 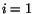 is
satisfied identically. For
is
satisfied identically. For 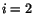 and
and 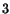 we obtain
we obtain
and, of course,
A solution of these is
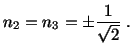 |
(4.5.17) |
For the values of 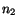 and
and 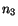 given by (4.5.17) and
given by (4.5.17) and 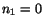 ,
eqn. (4.5.13) gives
,
eqn. (4.5.13) gives
and hence
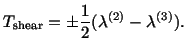 |
(4.5.18) |
Similarly for 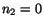 , a solution of (4.5.15) and (4.5.16) is
, a solution of (4.5.15) and (4.5.16) is
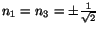 and the shear stress on this plane is
and the shear stress on this plane is
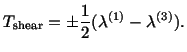 |
(4.5.19) |
For 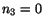 , a solution of (4.5.15) and (4.5.16) is
, a solution of (4.5.15) and (4.5.16) is
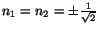 and the shear stress on this plane is
and the shear stress on this plane is
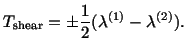 |
(4.5.20) |
Thus the extreme values of the shear stress are given by
(4.5.18),
(4.5.19) and (4.5.20). Note that on planes of maximum shear stress, the
normal stress need not be zero. In fact, the normal stress on the plane for
which
![]() in the present configuration
is kept fixed.
in the present configuration
is kept fixed.
![]() in the present configuration of the body, consider a plane whose
outer unit
normal is
in the present configuration of the body, consider a plane whose
outer unit
normal is
![]() . The stress vector
. The stress vector
![]() on this plane
given by equation (4.1.12) is
on this plane
given by equation (4.1.12) is ![]() . The normal stress on this plane is
given by
. The normal stress on this plane is
given by
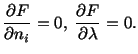
![]() and
and
![]() are uniquely determined and are
mutually orthogonal. However, when any two or all three of the principal
stresses are equal, then
are uniquely determined and are
mutually orthogonal. However, when any two or all three of the principal
stresses are equal, then
![]() and
and
![]() are not uniquely determined but can still be found so that
they are mutually orthogonal. Henceforth, in this section, we
will assume that the principal axes of the stress tensor are mutually
orthogonal.
are not uniquely determined but can still be found so that
they are mutually orthogonal. Henceforth, in this section, we
will assume that the principal axes of the stress tensor are mutually
orthogonal.
![]() axes along the principal axes of the stress, we see
that with respect to these axes
axes along the principal axes of the stress, we see
that with respect to these axes ![]() has the form
has the form
![$\displaystyle [T_{ij}] = \left[\begin{array}{ccc} \lambda^{(1)} & 0 & 0\\ 0 & \lambda^{(2)} & 0\\ 0 & 0 & \lambda^{(3)}\end{array}\right].$](img1339.gif)
![]() . Then, taking principal axes of stress as the
coordinate axes,
. Then, taking principal axes of stress as the
coordinate axes,
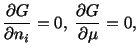
![]() and
and ![]() and the eqn. (4.5.16)
determine
and the eqn. (4.5.16)
determine ![]() and
and ![]() . A solution of these equations for which two out of
. A solution of these equations for which two out of
![]() and
and ![]() are zero is not interesting since this corresponds to
finding
are zero is not interesting since this corresponds to
finding
![]() on a principal plane which is zero. The
solution of (4.5.15) and (4.5.16) for which
on a principal plane which is zero. The
solution of (4.5.15) and (4.5.16) for which
![]() exists
only if
exists
only if
![]() . In this case too,
eqn. (4.5.13) gives
. In this case too,
eqn. (4.5.13) gives
![]() .
.
![]() and
and ![]() be
zero, say
be
zero, say
![]() ,
,
![]() . For this case, eqn. (4.5.15) for
. For this case, eqn. (4.5.15) for ![]() is
satisfied identically. For
is
satisfied identically. For ![]() and
and ![]() we obtain
we obtain