For a linear elastic solid or a Hookean material, it is assumed that the
Cauchy stress is a linear function of the infinitesimal strain. That is,
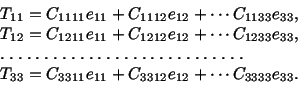 |
(5.2.1) |
We will assume that 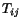 is symmetric and since
is symmetric and since 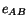 is
also symmetric, the above six equations can be written as
is
also symmetric, the above six equations can be written as
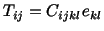 |
(5.2.2) |
in which
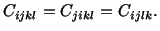 |
(5.2.3) |
Since 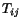 and
and 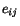 are components of second order tensors,
are components of second order tensors, 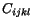 are components of a fourth-order tensor. It is known as the elasticity
tensor. It is this tensor which characterizes the mechanical properties of a
particular anisotropic Hookean elastic solid. The anisotropy of the material
is represented by the fact that the components of
are components of a fourth-order tensor. It is known as the elasticity
tensor. It is this tensor which characterizes the mechanical properties of a
particular anisotropic Hookean elastic solid. The anisotropy of the material
is represented by the fact that the components of 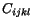 are in general
different for different choices of coordinate axes. If the body is
homogeneous, that is, the mechanical properties are the same for every
particle of the body, then
are in general
different for different choices of coordinate axes. If the body is
homogeneous, that is, the mechanical properties are the same for every
particle of the body, then 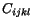 are constants (i.e. independent of
position). We shall only study homogeneous bodies.
are constants (i.e. independent of
position). We shall only study homogeneous bodies.
Because of the symmetry relations (5.2.3), the fourth order tensor 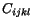 has 36 independent components. Thus, for a linear anisotropic elastic
material, we need no more than 36 material constants to specify its mechanical
properties.
has 36 independent components. Thus, for a linear anisotropic elastic
material, we need no more than 36 material constants to specify its mechanical
properties.
It follows from (5.2.1) that whenever
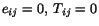 . Thus, in the
reference configuration, there is no stress. This implies that there are no
initial stresses present.
. Thus, in the
reference configuration, there is no stress. This implies that there are no
initial stresses present.
A material is said to be isotropic if its mechanical properties can be
described without reference to direction. That is, the components of the
elasticity tensor 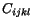 remain the same regardless of how the rectangular
Cartesian coordinate axes are rotated. In other words,
remain the same regardless of how the rectangular
Cartesian coordinate axes are rotated. In other words,
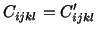 |
(5.2.4) |
under all orthogonal transformations of coordinate axes. A
tensor having the same components with respect to every orthonormal basis is
known as an isotropic tensor. An example of an isotropic tensor is
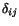 . It is obvious that the following three
fourth-order tensors are isotropic:
. It is obvious that the following three
fourth-order tensors are isotropic:
In fact, it can be shown that any fourth order isotropic tensor
can be represented as a linear combination of the above three tensors. Thus,
for an isotropic, linear elastic material, the stress-strain law (5.2.2) can
be written as
In order for the symmetry relation (5.2.3)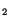 to hold,
to hold,
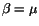 . Thus
. Thus
In the preceding equations 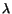 and
and 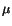 are constants.
Equation (5.2.5) is the constitutive equation for a linear elastic isotropic
material. The two material constants
are constants.
Equation (5.2.5) is the constitutive equation for a linear elastic isotropic
material. The two material constants 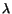 and
and 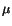 are known as
Lame's constants. Since
are known as
Lame's constants. Since 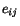 are dimensionless,
are dimensionless, 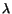 and
and 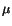 are of the same dimensions as the stress tensor, force per unit area. For a
given material, the values of Lamé's constants are to be determined from
suitable experiments.
are of the same dimensions as the stress tensor, force per unit area. For a
given material, the values of Lamé's constants are to be determined from
suitable experiments.
We now write (5.2.5) in a form usually studied in the Mechanics of Deformable
Bodies course. Taking the trace of both sides of (5.2.5) we obtain
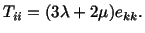 |
(5.2.6) |
Assuming that
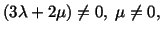 |
(5.2.7) |
we get
and hence
![$\displaystyle e_{ij} = \frac{1}{2\mu}\left[T_{ij} - \frac{\lambda}{3\lambda + 2\mu} T_{kk}\delta_{ij}\right]\ .$](img1392.gif) |
(5.2.8) |
To get a physical interpretation of Lamé's constants in terms
of Young's modulus 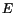 and Poisson's ratio
and Poisson's ratio 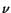 , we note that, in a simple
tension test, with the axial load
, we note that, in a simple
tension test, with the axial load  applied along
applied along 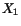 -axis,
-axis,
where 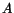 is the area of cross-section of the prismatic body. Also
is the area of cross-section of the prismatic body. Also
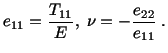 |
(5.2.9) |
Substituting for 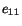 and
and 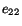 from (5.2.8) into
(5.2.9) and assuming that
from (5.2.8) into
(5.2.9) and assuming that
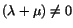 we arrive at
we arrive at
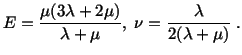 |
(5.2.10) |
The elimination of 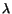 from these two equations gives
from these two equations gives
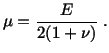 |
(5.2.11) |
In order for a tensile load to produce extension in the
direction of loading, it is clear from (5.2.9)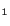 that
that 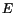 must be
must be 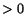 .
.
Another stress state, called simple shear, is the one for which
all stress components except one pair of off-diagonal elements
vanish. In particular, we choose
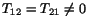 . Equation (5.2.8)
gives
. Equation (5.2.8)
gives
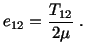 |
(5.2.12) |
In order for a simple shear force on 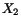 plane to produce a
sliding of the
plane to produce a
sliding of the 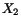 plane in the direction of the applied
load,
plane in the direction of the applied
load, 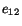 and
and 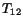 must be of the same sign. For that to be true,
must be of the same sign. For that to be true, 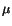 must be
must be 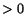 .
.
For 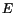 and
and 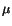 to be positive, it follows from (5.2.11) that
to be positive, it follows from (5.2.11) that 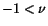 . Now
consider a stress state called, hydrostatic stress, for which
. Now
consider a stress state called, hydrostatic stress, for which
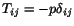 . For this case, equation (5.2.8) gives
. For this case, equation (5.2.8) gives
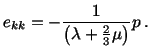 |
(5.2.13) |
Since
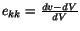 , therefore, in order for the
hydrostatic pressure to produce a decrease in volume, we must have
, therefore, in order for the
hydrostatic pressure to produce a decrease in volume, we must have
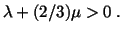 |
(5.2.14) |
Substituting in this equation from (5.2.10), we obtain
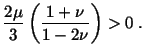 |
(5.2.15) |
On the assumption that 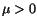 ,
, 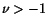 , the inequality
(5.2.15) implies that
, the inequality
(5.2.15) implies that 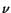 must be
must be 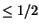 . Rewriting (5.2.13) as
. Rewriting (5.2.13) as
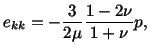 |
(5.2.16) |
we see that for
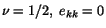 . That is, there is no
change in volume. Since for incompressible materials
. That is, there is no
change in volume. Since for incompressible materials
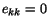 , therefore,
, therefore,
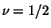 for incompressible materials.
for incompressible materials.
Equations (5.2.10), (5.2.11) and (5.2.5) yield
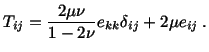 |
(5.2.17) |
For an incompressible material, the first term on the
right-hand side of (5.2.17) is of the form % and hence is indeterminate. It
is usually denoted by
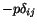 and the constitutive relation for an
incompressible linear elastic material becomes
and the constitutive relation for an
incompressible linear elastic material becomes
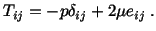 |
(5.2.18) |
Here 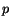 is called the hydrostatic pressure, and it can not be
determined from the strain field. However, whenever surface tractions are
prescribed on at least a part of the boundary,
is called the hydrostatic pressure, and it can not be
determined from the strain field. However, whenever surface tractions are
prescribed on at least a part of the boundary, 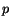 can be uniquely determined.
can be uniquely determined.
Example:
- a)
- For an isotropic Hookean material, show that the
principal axes of stress and strain coincide.
- b)
- Find a relation between the principal values of stress and strain.
Solution: Note that eigenvectors of 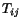 and
and 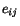 are the principal axes of stress and strain respectively.
are the principal axes of stress and strain respectively.
Let
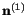 be an eigenvector of
be an eigenvector of 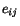 and
and 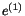 be the
corresponding eigenvalue. That is
be the
corresponding eigenvalue. That is
By Hooke's law we have
Therefore,
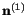 is also an eigenvector of
is also an eigenvector of 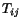 and the corresponding eigenvalue is
and the corresponding eigenvalue is
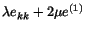 .
.
b) It is clear from eqn. (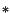 ) that the eigenvalue
) that the eigenvalue 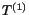 of
of
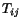 corresponding to the eigenvector
corresponding to the eigenvector
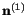 is
is
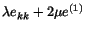 . Since
. Since
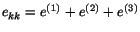 , therefore,
, therefore,
Similarly,
Exercise: (Recall the exercise given on page 2-11). For
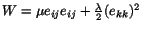 , show that
, show that
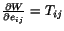 .
.
Hint: It is advisable to do the problem long-hand. That
is, first expand the given expression for 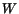 . Substitute
. Substitute
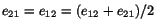 etc. in it and then carry out the differentiation with
respect to
etc. in it and then carry out the differentiation with
respect to
 etc.
etc.
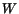 is called the stored energy function or the strain energy
density.
is called the stored energy function or the strain energy
density.
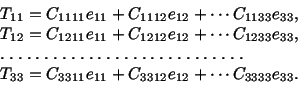
![]() and
and ![]() are components of second order tensors,
are components of second order tensors, ![]() are components of a fourth-order tensor. It is known as the elasticity
tensor. It is this tensor which characterizes the mechanical properties of a
particular anisotropic Hookean elastic solid. The anisotropy of the material
is represented by the fact that the components of
are components of a fourth-order tensor. It is known as the elasticity
tensor. It is this tensor which characterizes the mechanical properties of a
particular anisotropic Hookean elastic solid. The anisotropy of the material
is represented by the fact that the components of ![]() are in general
different for different choices of coordinate axes. If the body is
homogeneous, that is, the mechanical properties are the same for every
particle of the body, then
are in general
different for different choices of coordinate axes. If the body is
homogeneous, that is, the mechanical properties are the same for every
particle of the body, then ![]() are constants (i.e. independent of
position). We shall only study homogeneous bodies.
are constants (i.e. independent of
position). We shall only study homogeneous bodies.
![]() has 36 independent components. Thus, for a linear anisotropic elastic
material, we need no more than 36 material constants to specify its mechanical
properties.
has 36 independent components. Thus, for a linear anisotropic elastic
material, we need no more than 36 material constants to specify its mechanical
properties.
![]() . Thus, in the
reference configuration, there is no stress. This implies that there are no
initial stresses present.
. Thus, in the
reference configuration, there is no stress. This implies that there are no
initial stresses present.
![]() remain the same regardless of how the rectangular
Cartesian coordinate axes are rotated. In other words,
remain the same regardless of how the rectangular
Cartesian coordinate axes are rotated. In other words,
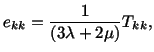
![$\displaystyle e_{ij} = \frac{1}{2\mu}\left[T_{ij} - \frac{\lambda}{3\lambda + 2\mu} T_{kk}\delta_{ij}\right]\ .$](img1392.gif)
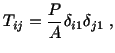
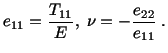
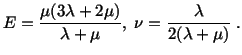
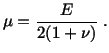
![]() . Equation (5.2.8)
gives
. Equation (5.2.8)
gives
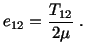
![]() and
and ![]() to be positive, it follows from (5.2.11) that
to be positive, it follows from (5.2.11) that ![]() . Now
consider a stress state called, hydrostatic stress, for which
. Now
consider a stress state called, hydrostatic stress, for which
![]() . For this case, equation (5.2.8) gives
. For this case, equation (5.2.8) gives
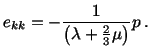
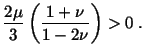
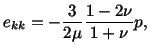
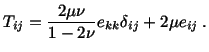
![]() and
and ![]() are the principal axes of stress and strain respectively.
are the principal axes of stress and strain respectively.
![]() be an eigenvector of
be an eigenvector of ![]() and
and ![]() be the
corresponding eigenvalue. That is
be the
corresponding eigenvalue. That is
![]() ) that the eigenvalue
) that the eigenvalue ![]() of
of
![]() corresponding to the eigenvector
corresponding to the eigenvector
![]() is
is
![]() . Since
. Since
![]() , therefore,
, therefore,
![]() , show that
, show that
![]() .
.
![]() . Substitute
. Substitute
![]() etc. in it and then carry out the differentiation with
respect to
etc. in it and then carry out the differentiation with
respect to
![]() etc.
etc.
![]() is called the stored energy function or the strain energy
density.
is called the stored energy function or the strain energy
density.