We shall consider only the case of small strains, and
infinitesimal velocities and
accelerations as compared to some reference values. Thus every particle is
always in a small neighborhood of the reference
configuration. The reference configuration in which
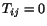 is also
called a natural state. Thus, if
is also
called a natural state. Thus, if 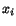 denotes the position in the natural
state of a typical material particle, we assume that
denotes the position in the natural
state of a typical material particle, we assume that
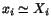 , and
that the magnitude of the components of the displacement gradient
, and
that the magnitude of the components of the displacement gradient
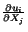 is much smaller than unity. Since
is much smaller than unity. Since
we have
Similarly,
Therefore, for small deformations,
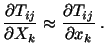 |
(5.3.1) |
Since
and
we have
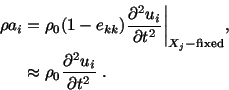 |
(5.3.2) |
Also
Thus the balance laws or conservation laws
for small deformations of a body take the
following form.
| |
Balance of mass: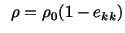 |
(5.3.3) |
| |
Balance of linear momentum: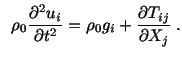 |
(5.3.4) |
For a linear elastic homogeneous and isotropic
body, substitution from
(5.2.5) and (3.14.3) into (5.3.4) gives
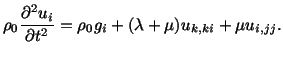 |
(5.3.5) |
These are three equations for the three unknowns 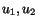 , and
, and 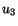 .
After a
solution of (5.3.5) has been obtained, one can find the present mass density
from eqn. (5.3.3). Note that eqn. (5.3.5) is a system of three coupled
partial
differential equations. In order to find a solution of (5.3.5) applicable to
a given problem, side conditions such as initial conditions and
boundary conditions are needed.
.
After a
solution of (5.3.5) has been obtained, one can find the present mass density
from eqn. (5.3.3). Note that eqn. (5.3.5) is a system of three coupled
partial
differential equations. In order to find a solution of (5.3.5) applicable to
a given problem, side conditions such as initial conditions and
boundary conditions are needed.
In a dynamic problem, one needs the values of
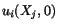 and
and
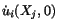 . That is, the initial displacement and the initial velocity field
should be given as smooth functions throughout the body.
Note that these initial conditions are not needed in a static problem.
However, in both static and dynamic problems one needs boundary conditions
which can be one of the following three types. In the boundary
condition of
traction the stress vector is prescribed at the
boundary points of the body. That is, at the points on the boundary
. That is, the initial displacement and the initial velocity field
should be given as smooth functions throughout the body.
Note that these initial conditions are not needed in a static problem.
However, in both static and dynamic problems one needs boundary conditions
which can be one of the following three types. In the boundary
condition of
traction the stress vector is prescribed at the
boundary points of the body. That is, at the points on the boundary
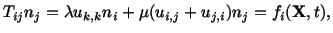 |
(5.3.6) |
in which 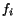 is a known function.
is a known function.
In a displacement type boundary condition, displacements are prescribed
on the boundary points. For example, a part of the boundary of
a body could be glued to a rigid support. In this case, displacements for
these
boundary points will be zero. The third type of boundary condition is the
one in which surface tractions are prescribed on one part and the displacements
on the remainder or at a boundary point, tangential components of the
stress-vector
and the normal component of the displacement vector
(or vice-versa) are prescribed. These are
known as the mixed type boundary conditions.
![]() is also
called a natural state. Thus, if
is also
called a natural state. Thus, if ![]() denotes the position in the natural
state of a typical material particle, we assume that
denotes the position in the natural
state of a typical material particle, we assume that
![]() , and
that the magnitude of the components of the displacement gradient
, and
that the magnitude of the components of the displacement gradient
![]() is much smaller than unity. Since
is much smaller than unity. Since
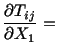
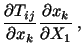
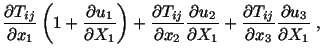
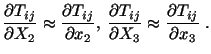
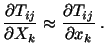
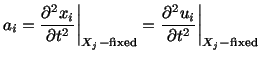
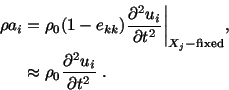
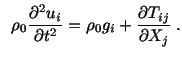
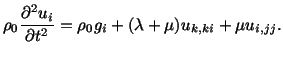
![]() , and
, and ![]() .
After a
solution of (5.3.5) has been obtained, one can find the present mass density
from eqn. (5.3.3). Note that eqn. (5.3.5) is a system of three coupled
partial
differential equations. In order to find a solution of (5.3.5) applicable to
a given problem, side conditions such as initial conditions and
boundary conditions are needed.
.
After a
solution of (5.3.5) has been obtained, one can find the present mass density
from eqn. (5.3.3). Note that eqn. (5.3.5) is a system of three coupled
partial
differential equations. In order to find a solution of (5.3.5) applicable to
a given problem, side conditions such as initial conditions and
boundary conditions are needed.
![]() and
and
![]() . That is, the initial displacement and the initial velocity field
should be given as smooth functions throughout the body.
Note that these initial conditions are not needed in a static problem.
However, in both static and dynamic problems one needs boundary conditions
which can be one of the following three types. In the boundary
condition of
traction the stress vector is prescribed at the
boundary points of the body. That is, at the points on the boundary
. That is, the initial displacement and the initial velocity field
should be given as smooth functions throughout the body.
Note that these initial conditions are not needed in a static problem.
However, in both static and dynamic problems one needs boundary conditions
which can be one of the following three types. In the boundary
condition of
traction the stress vector is prescribed at the
boundary points of the body. That is, at the points on the boundary