Next: A Uniqueness Theorem Up: The Linear Elastic Material Previous: Equations of the Infinitesimal
Let ![]() and
and ![]() be two possible displacement fields
corresponding to the body force fields
be two possible displacement fields
corresponding to the body force fields ![]() and
and ![]() and surface
tractions
and surface
tractions ![]() and
and ![]() respectively. Let
respectively. Let
![]() and
and
![]() be the stress fields corresponding to displacement fields
be the stress fields corresponding to displacement fields
![]() and
and ![]() . Then
. Then
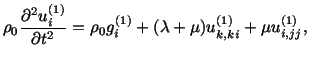 |
(5.4.1) | |
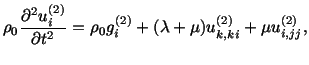 |
(5.4.2) | |
| either |
(5.4.3) | |
| either |
(5.4.4) |
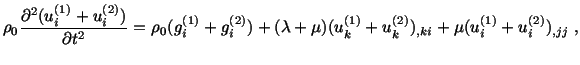 |
||
| either |
Thus
![]() is a possible motion for the same linear elastic
body corresponding to the body force
is a possible motion for the same linear elastic
body corresponding to the body force
![]() and surface
tractions
and surface
tractions
![]() . This is the principle of superposition
and is frequently used in the Mechanics of Materials course when
solving problems for the combined loads.
. This is the principle of superposition
and is frequently used in the Mechanics of Materials course when
solving problems for the combined loads.
One application of this principle in linear elastic problems is that in a given problem, we shall often assume that the body force is absent having in mind that its effect, if not negligible, can always be obtained separately and then superposed onto the solution of the problem with vanishing body force.