Equations (5.3.5) subject to given initial and
boundary conditions have a unique solution.
Assume that there exist two solutions 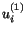 and
and 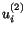 of eqn. (5.3.5) subject to the same initial and boundary conditions. Then
of eqn. (5.3.5) subject to the same initial and boundary conditions. Then
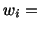 |
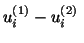 will be a solution of will be a solution of |
|
| |
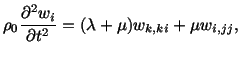 |
(5.5.1) |
and, on the boundary, either
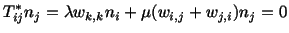 |
(5.5.2) |
or
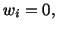 |
(5.5.3) |
and
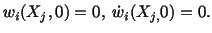 |
(5.5.4) |
Taking the inner product of (5.5.1) with
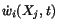 , integrating the
resulting equation over the region
, integrating the
resulting equation over the region  occupied by the body in the reference
configuration and by using the divergence theorem, we arrive at
occupied by the body in the reference
configuration and by using the divergence theorem, we arrive at
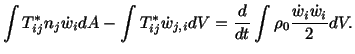 |
(5.5.5) |
The first integral vanishes because of (5.5.2) and (5.5.3). The
second integral can be rearranged to read
in which
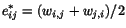 . Thus eqn. (5.5.5) becomes
. Thus eqn. (5.5.5) becomes
![$\displaystyle \frac{d}{dt}\int\left[\frac{\lambda}{2}e^\ast_{kk}e^\ast_{ii} + \mu e^\ast_{ij}e^\ast_{ij} + \frac{\rho_0}{2}\dot w_i\dot w_i\right]dV = 0.$](img1489.gif) |
(5.5.6) |
Integrating this and making use of the initial conditions
(5.5.4) for 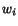 , we obtain
, we obtain
![$\displaystyle \int\left[\frac{\lambda}{2}e^\ast_{kk}e^\ast_{ii} + \mu e^\ast_{ij}e^\ast_{ij} + \frac{\rho_0}{2}\dot w_i\dot w_i\right] dV = 0.$](img1491.gif) |
(5.5.7) |
Noting that the integrand can be written as
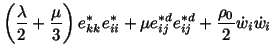 |
(5.5.8) |
in which
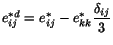 , we see that every term in (5.5.8) is
positive provided that
, we see that every term in (5.5.8) is
positive provided that
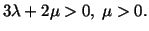 |
(5.5.9) |
We will henceforth assume that 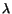 and
and 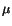 satisfy
(5.5.9). Thus for eqn. (5.5.7) to hold,
satisfy
(5.5.9). Thus for eqn. (5.5.7) to hold,
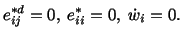 |
(5.5.10) |
Since 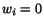 initially, therefore,
initially, therefore,
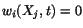 which
implies that
which
implies that
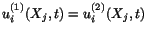 .
.
Thus if somehow one can find a solution of eqn. (5.3.5) that satisfies the
prescribed initial and boundary conditions, then that is the only solution of
eqn. (5.3.5). There are very few dynamic problems that have been solved.
In a static problem or, more appropriately, in a quasi-static problem, the
left-hand side of eqn. (5.3.5) becomes zero and one needs only the prescribed
boundary conditions. Thus the difference solution
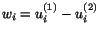 will satisfy
will satisfy
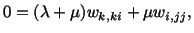 |
(5.5.11) |
and either (5.5.2) or (5.5.3) on the boundary. Taking the inner
product of (5.5.11) with 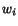 , integrating the resulting equation over
, integrating the resulting equation over 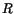 ,
and using the divergence theorem we arrive at
,
and using the divergence theorem we arrive at
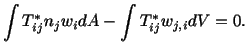 |
(5.5.12) |
The first integral vanishes because of (5.5.2) and (5.5.3) and
the second integral can be written as
![$\displaystyle \int\left[\left(\frac{\lambda}{2} + \frac{\mu}{3}\right) e^\ast_{kk} e^\ast_{ii} + \mu e^{\ast d}_{ij} e^{\ast d}_{ij}\right] dV = 0.$](img1502.gif) |
(5.5.13) |
For this equation to hold,
and hence
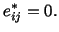 |
(5.5.14) |
A solution of eqn. (5.5.14) given in Section 3.14 is
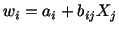 |
(5.5.15) |
in which 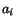 and
and
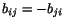 are constants. If
displacements are prescribed at three noncolinear points on the boundary, then
are constants. If
displacements are prescribed at three noncolinear points on the boundary, then
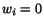 and the solution of the given boundary value problem is unique.
However, if surface tractions are prescribed on all of the boundary, then
different solutions of the same boundary value problem can differ at most by a
rigid body motion. Even though the two displacement fields differ by a rigid
body motion, the stress fields and the strain fields obtained from such
displacement fields are identical.
and the solution of the given boundary value problem is unique.
However, if surface tractions are prescribed on all of the boundary, then
different solutions of the same boundary value problem can differ at most by a
rigid body motion. Even though the two displacement fields differ by a rigid
body motion, the stress fields and the strain fields obtained from such
displacement fields are identical.
![]() and
and ![]() of eqn. (5.3.5) subject to the same initial and boundary conditions. Then
of eqn. (5.3.5) subject to the same initial and boundary conditions. Then
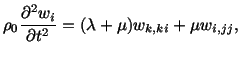
![]() , integrating the
resulting equation over the region
, integrating the
resulting equation over the region ![]() occupied by the body in the reference
configuration and by using the divergence theorem, we arrive at
occupied by the body in the reference
configuration and by using the divergence theorem, we arrive at
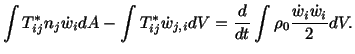
![$\displaystyle \frac{d}{dt}\int\left[\frac{\lambda}{2}w_{k,k}w_{i,i} + \mu e^\ast_{ij}e^\ast_{ij}\right]dV,$](img1487.gif)
![$\displaystyle \frac{d}{dt}\int\left[\frac{\lambda}{2}e^\ast_{kk}e^\ast_{ii} + \mu e^\ast_{ij}e^\ast_{ij} + \frac{\rho_0}{2}\dot w_i\dot w_i\right]dV = 0.$](img1489.gif)
![$\displaystyle \int\left[\frac{\lambda}{2}e^\ast_{kk}e^\ast_{ii} + \mu e^\ast_{ij}e^\ast_{ij} + \frac{\rho_0}{2}\dot w_i\dot w_i\right] dV = 0.$](img1491.gif)
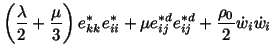
![]() will satisfy
will satisfy
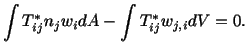
![$\displaystyle \int\left[\left(\frac{\lambda}{2} + \frac{\mu}{3}\right) e^\ast_{kk} e^\ast_{ii} + \mu e^{\ast d}_{ij} e^{\ast d}_{ij}\right] dV = 0.$](img1502.gif)