Next: Some Examples Up: The Linear Elastic Material Previous: A Uniqueness Theorem
In static problems where the surface tractions are prescribed on the entire boundary, it is convenient to solve the equations of equilibrium
| (5.6.1) |
![$\displaystyle \frac{1}{2\mu} [T_{ij,kp} + T_{kj,ij} - T_{ip,jk} - T_{jk,ip}]$](img1509.gif) |
||
![$\displaystyle \hspace*{.3in} -\frac{\lambda}{2\mu (3\lambda + 2\mu )}[\delta_{i...
...kp} + T_{mm,ij} \delta_{kp} - T_{mm,ip}\delta_{jk} - T_{mm,jk}\delta_{ip}] = 0.$](img1510.gif) |
(5.6.2) |
![$\displaystyle T_{ij,kk} + T_{kk,ij} - T_{ik,jk} - T_{jk,ik} = \frac{\lambda}{3\lambda + 2\mu} [T_{mm,kk} \delta_{ij} + T_{mm,ij}].$](img1512.gif) |
(5.6.3) |
In solid mechanics problems, it is usual to neglect the effect of gravity and write (5.6.1) as
| (5.6.4) |
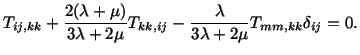 |
(5.6.5) |
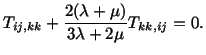 |
(5.6.6) |
These are the compatibility equations in the absence of body forces. Thus for a stress field to be a solution of a static problem with zero body force for a homogeneous and isotropic linear elastic body, it must satisfy
Note that if ![]() satisfies (a) and (c) but not (b), then that
satisfies (a) and (c) but not (b), then that ![]() will not correspond to a stress field in a linear elastic body since
will not correspond to a stress field in a linear elastic body since ![]() corresponding to such a
corresponding to such a ![]() will not result in a unique
will not result in a unique ![]() .
.
Exercise: Can the following stress field represent a possible solution of a static problem with zero body force for a homogeneous and isotropic linear elastic body?
Example: For a plane stress state, express the compatibility conditions in terms of a stress function.
Solution: Recall the second exercise given on page 4-9. For a plane stress state,
| (5.6.7) |
| (5.6.8) |
| (5.6.9) |
Exercise: Show that for plane strain problems (i.e., those
for which
![]() with zero body
force there is only one independent compatibility condition in terms of the
components of the stress and this can be written as
with zero body
force there is only one independent compatibility condition in terms of the
components of the stress and this can be written as
| (5.6.10) |
Exercise: (a) Simplify the equations of equilibrium with zero body force for plane strain problems. (b) Introduce a function
| (5.6.11) |
Note that for plane strain case ![]() need not and, in general, will not
vanish. If we substitute the stress field given by (5.6.11) into (5.6.10)
we arrive at (5.6.9). Thus the task of finding a
solution of a static plane strain problem also
reduces to that of finding a solution of (5.6.9) which satisfies the pertinent
boundary conditions.
need not and, in general, will not
vanish. If we substitute the stress field given by (5.6.11) into (5.6.10)
we arrive at (5.6.9). Thus the task of finding a
solution of a static plane strain problem also
reduces to that of finding a solution of (5.6.9) which satisfies the pertinent
boundary conditions.