(a) Vibration of an Infinite Plate
Consider an infinite plate bounded by the planes 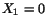 and
and
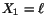 .
The vibrations of the plate are caused by a prescribed motion of these
bounding planes or by prescribed surface tractions on these planes. Since we
study steady state vibration of the plate, the
initial displacement and velocity fields in the plate are not required.
We will neglect the
effect of gravity in these problems.
.
The vibrations of the plate are caused by a prescribed motion of these
bounding planes or by prescribed surface tractions on these planes. Since we
study steady state vibration of the plate, the
initial displacement and velocity fields in the plate are not required.
We will neglect the
effect of gravity in these problems.
We begin by assuming that the displacement field in the plate is of the form
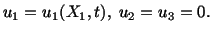 |
(5.7.1) |
For this displacement field, the equations of motion (5.3.5)
reduce to the following equation
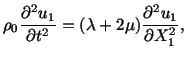 |
(5.7.2) |
which can be rewritten as
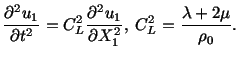 |
(5.7.3) |
A steady state vibration solution to this equation is of the form
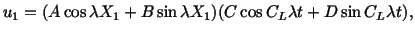 |
(5.7.4) |
where the constants
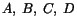 and
and 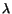 are
determined by boundary conditions. This vibration mode is sometimes termed a
``thickness stretch'' because the plate is being stretched
through its thickness. It is analogous to acoustic vibration of organ pipes
and to the longitudinal vibration of slender rods.
are
determined by boundary conditions. This vibration mode is sometimes termed a
``thickness stretch'' because the plate is being stretched
through its thickness. It is analogous to acoustic vibration of organ pipes
and to the longitudinal vibration of slender rods.
Another vibration mode can be obtained by assuming the displacement field
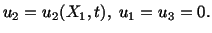 |
(5.7.5) |
In this case, the displacement field must satisfy the equation
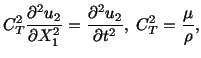 |
(5.7.6) |
and the solution is of the same form as in the previous case.
This vibration is termed ``thickness shear'' and it is analogous to the
motion of a vibrating string.
Example 5.7.1: (a) Find the thickness-stretch vibration of
a plate, where the left face 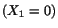 is subjected to a forced displacement
is subjected to a forced displacement
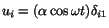 and the right face
and the right face
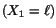 is
fixed.
is
fixed.
(b) Determine the values of 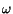 that give resonance.
that give resonance.
Solution: (a) The boundary condition on the left face
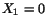 and eqn. (5.7.4) give
and eqn. (5.7.4) give
Therefore,
The second boundary condition gives
Therefore,
and the vibration is given by
(b) Resonance is indicated by unbounded displacements. This occurs
in part (a) for forcing frequencies corresponding to
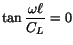 , that is, when
, that is, when
Example 5.7.2 (a) Find the thickness-shear vibration of an
infinite plate which has an applied surface traction
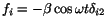 on the plane
on the plane 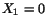 and is fixed on the plane
and is fixed on the plane
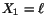 .
.
(b) Determine the resonant frequencies.
Solution: On the plane 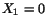 ,
,
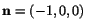 . Therefore
. Therefore
gives
This shearing stress forces a vibration of the form
Using Hooke's law (5.2.5), we have
Therefore
Thus
The boundary condition at
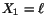 gives
gives
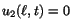 .
.
Hence
Thus
(b) Resonance occurs for
or
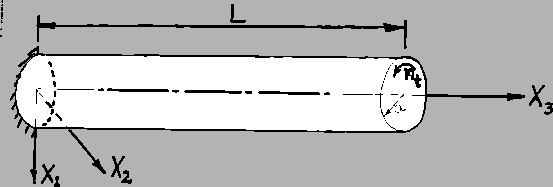
(B) Torsion of a Circular Shaft
Consider elastic deformations of a cylindrical bar of circular
cross-section of radius 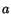 and length
and length 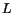 , that is being twisted by an end
moment
, that is being twisted by an end
moment 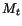 at the right end and is fixed at the left end. We choose the
at the right end and is fixed at the left end. We choose the
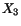 -axis to coincide with the axis of the cylinder and the left-hand and
right-hand faces to correspond to the planes
-axis to coincide with the axis of the cylinder and the left-hand and
right-hand faces to correspond to the planes 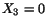 and
and 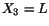 respectively.
respectively.
This problem involves the solution of equilibrium equations
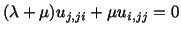 |
(5.7.7) |
subject to the boundary conditions
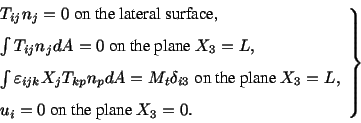 |
(5.7.8) |
Note that if the problem is formulated in terms of displacements, then
compatibility conditions (5.6.6) are not needed. We use St. Venant's
semi-inverse method to solve the problem in
an inverse way. That is, we make a kinematic assumption about the
displacement field and then ensure that eqns. (5.7.7) and (5.7.8) are
satisfied.
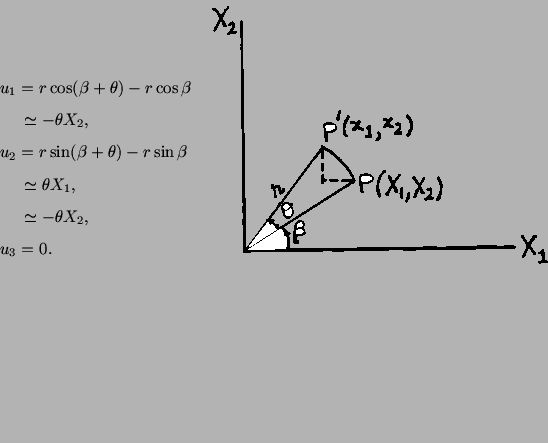
Because of the symmetry of the problem, it is reasonable to assume that the
motion of each cross-sectional plane induced by the end moments is a rigid
body motion about the
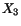 -axis. This motion is similar to that of a stack of coins in which
each coin is rotated by a slightly different angle than the previous coin. We
will see that this assumption results in a displacement field that satisfies
(5.7.7) and (5.7.8). To ensure that the deformations are small, we will
assume that the angle
-axis. This motion is similar to that of a stack of coins in which
each coin is rotated by a slightly different angle than the previous coin. We
will see that this assumption results in a displacement field that satisfies
(5.7.7) and (5.7.8). To ensure that the deformations are small, we will
assume that the angle 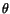 of rotation of any section with respect to the
left-end is very small as compared to one.
of rotation of any section with respect to the
left-end is very small as compared to one.
Under the preceding assumptions, the displacement of any point can be
calculated as follows.
For this displacement field to satisfy the equations of
equilibrium (5.7.7), we must have
Thus
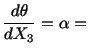 constant constant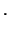 |
(5.7.9) |
That is, the angle of twist per unit length is the same over the
entire length of the shaft. From (5.7.9) and recalling that
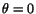 at
at
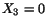 , we get
, we get
and, therefore,
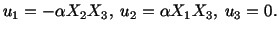 |
(5.7.10) |
The strains and stresses associated with these
displacements can be calculated from eqns. (3.14.3) and (5.2.5). The
non-zero components of strains are
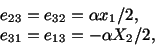 |
(5.7.11) |
and the non-zero components of stress are
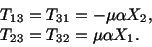 |
(5.7.12) |
To see whether the boundary conditions are satisfied or not, we note that on
the lateral surface a unit outer normal
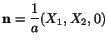 . Therefore, on the lateral surface,
. Therefore, on the lateral surface,
and the calculated stress field does satisfy (5.7.8) . On
the end plane
. On
the end plane  ,
,
 and in order that (5.7.8)
and in order that (5.7.8) be satisfied,
be satisfied,
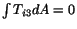 which is true because
which is true because
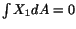 ,
,
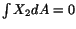 . The boundary condition (5.7.8)
. The boundary condition (5.7.8)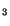 requires that, on the end
plane
requires that, on the end
plane 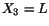 ,
,
This gives
or
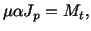 |
(5.7.13) |
in which 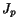 is the polar moment of inertia and equals
is the polar moment of inertia and equals 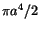 . The boundary condition (5.7.8)
. The boundary condition (5.7.8)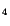 is clearly satisfied by the
displacement field (5.7.10).
is clearly satisfied by the
displacement field (5.7.10).
Substituting for 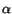 from (5.7.13) into (5.7.10), (5.7.11) and (5.7.12)
we obtain the displacement components, non-zero strain components and non-zero
stress components at any point in the cylindrical bar. In terms of the
twisting moment
from (5.7.13) into (5.7.10), (5.7.11) and (5.7.12)
we obtain the displacement components, non-zero strain components and non-zero
stress components at any point in the cylindrical bar. In terms of the
twisting moment 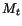 , the stress tensor becomes
, the stress tensor becomes
![\begin{equation*}[T_{ij}]= \frac{M_t}{J_p}\left[\begin{array}{ccc} 0 & 0 & -X_2\...
...0 & X_1\\ \noalign{\vskip .1in} -X_2 & X_1 & 0\end{array}\right]\end{equation*}](img1597.gif) |
(5.7.14) |
At any point
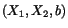 of a cross-section
of a cross-section
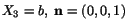 and the stress vector
and the stress vector
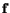 is given by
is given by
Note that
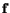 lies in the plane
lies in the plane 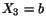 implying
thereby that there is no normal stress at any point on the plane
implying
thereby that there is no normal stress at any point on the plane 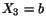 .
Also
.
Also
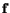 is perpendicular to the radius vector joining the point
is perpendicular to the radius vector joining the point
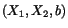 with the center
with the center 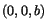 of the cross-section. The magnitude
of
of the cross-section. The magnitude
of
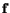 is
is
From this we see that the maximum stress is a tangential stress
that acts on the boundary of the cylinder and has the magnitude
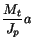 .
.
(c) Torsion of Non-Circular Cylinders
For cross-sections other than circular, the stress field (5.7.14) does not
satisfy the boundary conditions of zero tractions on the mantle of the
cylinder. We will see that in order for this boundary condition to be
satisfied, the cross-sections will not remain plane.
We begin by assuming a displacement field that still rotates each
cross-section by a small angle 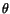 , but in addition there may be a
displacement in the axial direction. This warping of a cross-sectional
plane will be defined by
, but in addition there may be a
displacement in the axial direction. This warping of a cross-sectional
plane will be defined by
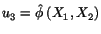 . Thus we assume that
each
cross-section is warped in the same way. For this to be true the left end of
the cylinder can not be fixed to a rigid flat support but is subjected to a
torque equal and opposite to that applied to the right end. The rigid motion
is removed by applying suitable constraints.
. Thus we assume that
each
cross-section is warped in the same way. For this to be true the left end of
the cylinder can not be fixed to a rigid flat support but is subjected to a
torque equal and opposite to that applied to the right end. The rigid motion
is removed by applying suitable constraints.
The assumed displacement field has the form
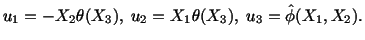 |
(5.7.15) |
For this displacement field to satisfy the equations of
equilibrium (5.7.7), we must have
Therefore, the angle 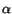 of twist per unit length is the same
over the entire length of the cylinder. Setting
of twist per unit length is the same
over the entire length of the cylinder. Setting
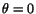 at
at 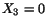 , we
get
, we
get
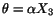 and therefore the displacement field (5.7.15) can be
rewritten as
and therefore the displacement field (5.7.15) can be
rewritten as
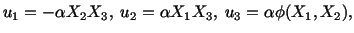 |
(5.7.17) |
where
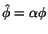 . For equilibrium,
. For equilibrium, 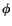 must satisfy
must satisfy
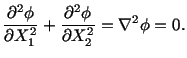 |
(5.7.18) |
Stresses corresponding to the displacements (5.7.17)
are
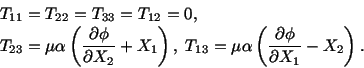 |
(5.7.19) |
Since the bar is cylindrical, the unit normal to the lateral
surface has the form
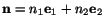 and the
associated surface traction is given by
and the
associated surface traction is given by
For the lateral surface to be traction free,
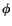 must satisfy
must satisfy
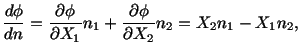 |
(5.7.20) |
on the boundary.
In order that the boundary condition (5.7.8)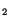 be satisfied,
be satisfied,
Now
because of (5.7.20). Using a similar argument one can show that
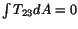 . The boundary condition (5.7.8)
. The boundary condition (5.7.8)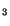 gives
gives
where
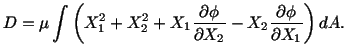 |
(5.7.22) |
The formula (5.7.21) shows that the twisting moment or torque
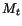 is proportional to the angle of twist per unit length, so that the
constant
is proportional to the angle of twist per unit length, so that the
constant 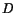 provides a measure of the rigidity of a bar subjected to torsion.
provides a measure of the rigidity of a bar subjected to torsion.
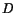 is called the torsional rigidity of the bar.
is called the torsional rigidity of the bar.
Hence the torsion problem is solved once 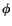 is determined by solving
(5.7.18) and (5.7.20).
is determined by solving
(5.7.18) and (5.7.20).
For an elliptic cylindrical bar with the cross-section given by
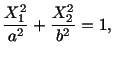 |
(5.7.23) |
we see that on the boundary,
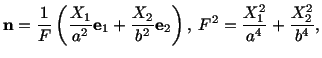 |
(5.7.24) |
and, therefore, eqn. (5.7.20) becomes
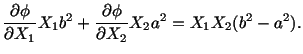 |
(5.7.25) |
This suggests that
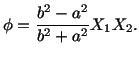 |
(5.7.26) |
This choice of 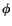 satisfies (5.7.25) and (5.7.18).
Substituting for
satisfies (5.7.25) and (5.7.18).
Substituting for 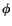 in (5.7.22) and then the result in (5.7.21) we arrive
at
in (5.7.22) and then the result in (5.7.21) we arrive
at
in which 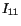 and
and 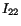 are, respectively,
the second moments of area
about
are, respectively,
the second moments of area
about 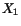 and
and 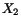 axes. Recalling that for an ellipse
axes. Recalling that for an ellipse
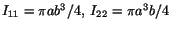 , we obtain
, we obtain
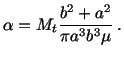 |
(5.7.27) |
Substitution for 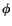 into (5.7.17) and (5.7.19) yields
into (5.7.17) and (5.7.19) yields
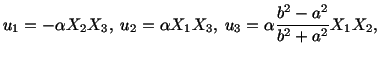 |
(5.7.28) |
and
At any point
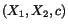 of a cross-section
of a cross-section
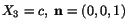 and the stress vector
and the stress vector
 is given by
is given by
Since
 lies in the plane
lies in the plane 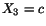 , therefore,
there is no normal stress at the point on the plane
, therefore,
there is no normal stress at the point on the plane 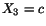 . The magnitude
of
. The magnitude
of
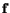 gives the shear stress
gives the shear stress 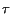 at the point.
at the point.
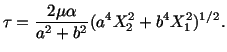 |
(5.7.30) |
A point in the interior of the cross-section where 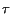 takes
on extremum values is given by
takes
on extremum values is given by
This gives
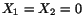 and at this point
and at this point 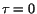 . To
find points on the boundary where
. To
find points on the boundary where 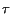 may have extremum values we first
write (5.7.30) as
may have extremum values we first
write (5.7.30) as
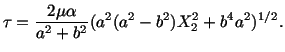 |
(5.7.31) |
Since 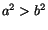 , it is obvious that
, it is obvious that 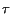 is minimum at
is minimum at 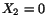 and has the value
and has the value
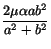 .
. 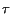 is maximum at
is maximum at
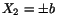 and has the value
and has the value
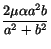 . Thus, the maximum shear stress occurs at the extremities
of the minor axis of the ellipse, contrary to the intuitive expectation that
the maximum shear stress would occur at points of maximum curvature.
. Thus, the maximum shear stress occurs at the extremities
of the minor axis of the ellipse, contrary to the intuitive expectation that
the maximum shear stress would occur at points of maximum curvature.
It is clear from (5.7.28)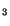 that the axial displacement of
points in the first and third quadrant will
be along the
that the axial displacement of
points in the first and third quadrant will
be along the 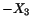 axis and that of points in the second and fourth
quadrant will be along the
axis and that of points in the second and fourth
quadrant will be along the 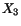 -axis.
The points which have the same displacement in
-axis.
The points which have the same displacement in 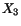 -direction lie
on a rectangular hyperbola.
-direction lie
on a rectangular hyperbola.
![]() and
and
![]() .
The vibrations of the plate are caused by a prescribed motion of these
bounding planes or by prescribed surface tractions on these planes. Since we
study steady state vibration of the plate, the
initial displacement and velocity fields in the plate are not required.
We will neglect the
effect of gravity in these problems.
.
The vibrations of the plate are caused by a prescribed motion of these
bounding planes or by prescribed surface tractions on these planes. Since we
study steady state vibration of the plate, the
initial displacement and velocity fields in the plate are not required.
We will neglect the
effect of gravity in these problems.
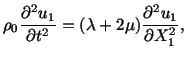
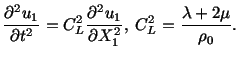
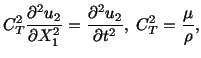
![]() is subjected to a forced displacement
is subjected to a forced displacement
![]() and the right face
and the right face
![]() is
fixed.
is
fixed.
![]() that give resonance.
that give resonance.
![]() and eqn. (5.7.4) give
and eqn. (5.7.4) give
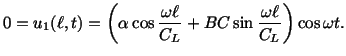
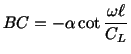
![$\displaystyle u_1(X_1,t) = \alpha \left[\cos\frac{\omega}{C_L}X_1 - \frac{\sin\...
...omega}{C_1}X_1}{\tan\displaystyle\frac{\omega\ell }{C_L}}\right] \cos \omega t.$](img1553.gif)
![]() , that is, when
, that is, when
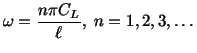
![]() on the plane
on the plane ![]() and is fixed on the plane
and is fixed on the plane
![]() .
.
![]() ,
,
![]() . Therefore
. Therefore
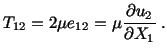
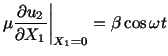
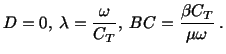
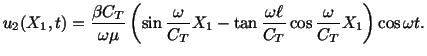
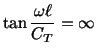

![]() and length
and length ![]() , that is being twisted by an end
moment
, that is being twisted by an end
moment ![]() at the right end and is fixed at the left end. We choose the
at the right end and is fixed at the left end. We choose the
![]() -axis to coincide with the axis of the cylinder and the left-hand and
right-hand faces to correspond to the planes
-axis to coincide with the axis of the cylinder and the left-hand and
right-hand faces to correspond to the planes ![]() and
and ![]() respectively.
respectively.
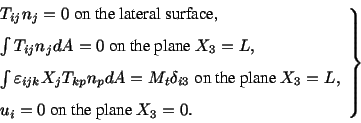
![]() -axis. This motion is similar to that of a stack of coins in which
each coin is rotated by a slightly different angle than the previous coin. We
will see that this assumption results in a displacement field that satisfies
(5.7.7) and (5.7.8). To ensure that the deformations are small, we will
assume that the angle
-axis. This motion is similar to that of a stack of coins in which
each coin is rotated by a slightly different angle than the previous coin. We
will see that this assumption results in a displacement field that satisfies
(5.7.7) and (5.7.8). To ensure that the deformations are small, we will
assume that the angle ![]() of rotation of any section with respect to the
left-end is very small as compared to one.
of rotation of any section with respect to the
left-end is very small as compared to one.
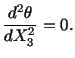
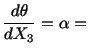 constant
constant![]() . Therefore, on the lateral surface,
. Therefore, on the lateral surface,
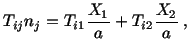
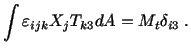
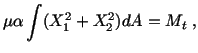
![]() from (5.7.13) into (5.7.10), (5.7.11) and (5.7.12)
we obtain the displacement components, non-zero strain components and non-zero
stress components at any point in the cylindrical bar. In terms of the
twisting moment
from (5.7.13) into (5.7.10), (5.7.11) and (5.7.12)
we obtain the displacement components, non-zero strain components and non-zero
stress components at any point in the cylindrical bar. In terms of the
twisting moment ![]() , the stress tensor becomes
, the stress tensor becomes
![\begin{equation*}[T_{ij}]= \frac{M_t}{J_p}\left[\begin{array}{ccc} 0 & 0 & -X_2\...
...0 & X_1\\ \noalign{\vskip .1in} -X_2 & X_1 & 0\end{array}\right]\end{equation*}](img1597.gif)
![]() of a cross-section
of a cross-section
![]() and the stress vector
and the stress vector
![]() is given by
is given by
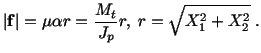
![]() , but in addition there may be a
displacement in the axial direction. This warping of a cross-sectional
plane will be defined by
, but in addition there may be a
displacement in the axial direction. This warping of a cross-sectional
plane will be defined by
![]() . Thus we assume that
each
cross-section is warped in the same way. For this to be true the left end of
the cylinder can not be fixed to a rigid flat support but is subjected to a
torque equal and opposite to that applied to the right end. The rigid motion
is removed by applying suitable constraints.
. Thus we assume that
each
cross-section is warped in the same way. For this to be true the left end of
the cylinder can not be fixed to a rigid flat support but is subjected to a
torque equal and opposite to that applied to the right end. The rigid motion
is removed by applying suitable constraints.
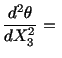
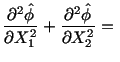
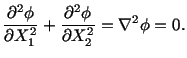
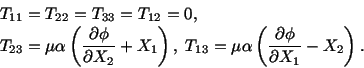
![$\displaystyle f_i = \mu\alpha \left[\left(\frac{\partial\phi}{\partial X_1} - X...
...1 + \left(\frac{\partial\phi}{\partial X_2} + X_1\right) n_2\right]\delta_{i3}.$](img1616.gif)
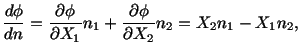
![]() be satisfied,
be satisfied,
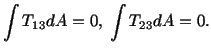
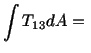
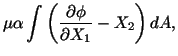
![$\displaystyle \mu\alpha\int\left[\frac{\partial}{\partial X_1} \left(X_1\left(\...
...\left(X_1\left(\frac{\partial\phi}{\partial X_2} + X_1\right)\right)\right] dA,$](img1621.gif)
![$\displaystyle \mu\alpha\oint X_1\left[\left(\frac{\partial\phi}{\partial X_1} -...
...right) n_1 + \left(\frac{\partial\phi}{\partial X_2} + X_1\right)n_2\right] ds,$](img1622.gif)
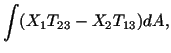
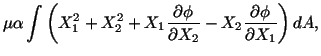
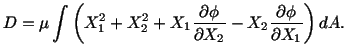
![]() is determined by solving
(5.7.18) and (5.7.20).
is determined by solving
(5.7.18) and (5.7.20).
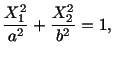
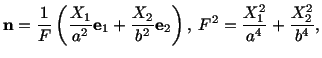
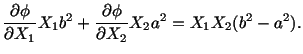
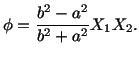
![$\displaystyle M_t = \frac{2\mu}{b^2 + a^2}[b^2I_{22} + a^2I_{11}]\alpha$](img1634.gif)
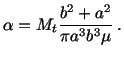
![]() into (5.7.17) and (5.7.19) yields
into (5.7.17) and (5.7.19) yields
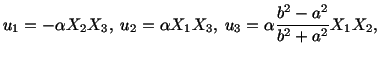
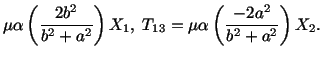
![]() of a cross-section
of a cross-section
![]() and the stress vector
and the stress vector
![]() is given by
is given by
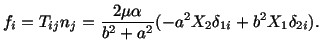
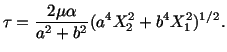
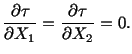
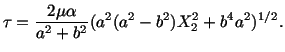
![]() that the axial displacement of
points in the first and third quadrant will
be along the
that the axial displacement of
points in the first and third quadrant will
be along the ![]() axis and that of points in the second and fourth
quadrant will be along the
axis and that of points in the second and fourth
quadrant will be along the ![]() -axis.
The points which have the same displacement in
-axis.
The points which have the same displacement in ![]() -direction lie
on a rectangular hyperbola.
-direction lie
on a rectangular hyperbola.