For a viscous material, the Cauchy stress tensor depends not only on the
deformation gradient but also on its time derivative. That is
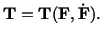 |
(6.1.1) |
Most fluids are isotropic and homogeneous; an exception being a
liquid crystal which is anisotropic. Here we will study isotropic fluids
only. For an isotropic fluid, equation (6.1.1) reduces to
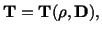 |
(6.1.2) |
and for a linear viscous fluid, we have
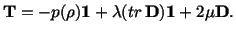 |
(6.1.3) |
Here 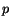 is the hydrostatic pressure,
is the hydrostatic pressure, 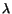 the bulk
viscosity and
the bulk
viscosity and 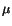 the shear viscosity. The word linear in linear viscous
fluid signifies that the viscous part of the stress (the last two terms on the
right-hand side of (6.1.3)) depends linearly upon the strain-rate tensor
the shear viscosity. The word linear in linear viscous
fluid signifies that the viscous part of the stress (the last two terms on the
right-hand side of (6.1.3)) depends linearly upon the strain-rate tensor
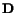 .
A perfect fluid or an ideal gas has
no viscosity, and therefore can be described by the constitutive relation
.
A perfect fluid or an ideal gas has
no viscosity, and therefore can be described by the constitutive relation
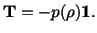 |
(6.1.4) |
Thus a perfect fluid is a nonlinear elastic material in the
sense that the Cauchy stress for it depends only on the present value of the
deformation gradient. For an ideal gas,
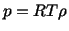 |
(6.1.5) |
where 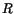 is the universal gas constant and
is the universal gas constant and 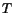 is the
temperature in degrees Kelvin. Thus for deformations of an ideal gas at a
constant temperature
is the
temperature in degrees Kelvin. Thus for deformations of an ideal gas at a
constant temperature
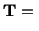 const. const.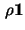 |
(6.1.6) |
and the value of the const. depends upon the gas and its temperature.
Equation (6.1.3) for
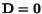 gives
gives
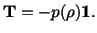 |
(6.1.7) |
Hence in a fluid at rest, the state of stress is a hydrostatic
pressure. Note that the state of stress in a perfect fluid or an ideal gas is
always that of hydrostatic pressure whether or not it is being deformed.
However, in a viscous fluid, no shear stress exists if and only if it is at
rest. This is sometimes taken as the definition of a viscous fluid; viz. a
viscous fluid at rest can not support any shear stresses. On the other hand,
a solid body when subjected to shear or tangential tractions can stay
stationary.
For a homogeneous fluid the viscosities 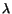 and
and 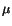 are constants.
Equation (6.1.3) implies that the principal axes of the stretching tensor or
the strain-rate tensor
are constants.
Equation (6.1.3) implies that the principal axes of the stretching tensor or
the strain-rate tensor
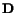 coincide with the principal axes of the
stress tensor
coincide with the principal axes of the
stress tensor
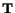 .
.
Whereas the constitutive relation (5.2.1) or (5.2.2) for a linear elastic
material describes well its infinitesimal deformations, no such restriction is
imposed on (6.1.3). Said differently, equation (6.1.3) describes deformations
of a viscous fluid for all values of the stretching tensor
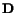 . The
material characterized by equation (6.1.3) is called a Navier-Stokes fluid.
Usually fluids and gases are assumed to be incompressible. The constitutive
relations for an incompressible ideal gas and an incompressible Navier-Stokes
fluid are respectively
. The
material characterized by equation (6.1.3) is called a Navier-Stokes fluid.
Usually fluids and gases are assumed to be incompressible. The constitutive
relations for an incompressible ideal gas and an incompressible Navier-Stokes
fluid are respectively
where the hydrostatic pressure 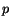 is not determined by the
deformation of the fluid. It is, however, determined by the boundary
conditions. Even for a homogeneous fluid, the pressure
is not determined by the
deformation of the fluid. It is, however, determined by the boundary
conditions. Even for a homogeneous fluid, the pressure 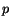 is a function of
the spatial coordinate
is a function of
the spatial coordinate
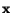 and time
and time 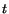 . In (6.1.9) we have used the
continuity condition,
. In (6.1.9) we have used the
continuity condition,
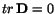 , for an incompressible fluid.
, for an incompressible fluid.
![]() gives
gives
![]() and
and ![]() are constants.
Equation (6.1.3) implies that the principal axes of the stretching tensor or
the strain-rate tensor
are constants.
Equation (6.1.3) implies that the principal axes of the stretching tensor or
the strain-rate tensor
![]() coincide with the principal axes of the
stress tensor
coincide with the principal axes of the
stress tensor
![]() .
.
![]() . The
material characterized by equation (6.1.3) is called a Navier-Stokes fluid.
Usually fluids and gases are assumed to be incompressible. The constitutive
relations for an incompressible ideal gas and an incompressible Navier-Stokes
fluid are respectively
. The
material characterized by equation (6.1.3) is called a Navier-Stokes fluid.
Usually fluids and gases are assumed to be incompressible. The constitutive
relations for an incompressible ideal gas and an incompressible Navier-Stokes
fluid are respectively