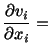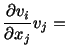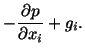One generally uses the spatial description of motion for a fluid. Thus the
balance of mass, and the balance of linear momentum for a compressible
Navier-Stokes fluid are
| |
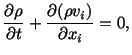 |
(6.2.1) |
| |
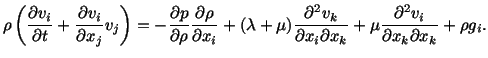 |
(6.2.2) |
Equation (6.2.2) is obtained by substituting into (4.1.14) for the
acceleration from (3.6.3) and for the Cauchy stress from (6.1.3). Because of
the presence of the convective part of the acceleration on the left-hand side
of (6.2.2), equations governing the motion of a fluid are nonlinear. In the
referential description of motion used to describe the deformations of a
solid, the acceleration is linear in displacements. Were we to use the
referential description of motion for studying the deformations of a fluid,
the expression for the strain-rate tensor
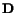 in terms of the spatial
gradients of the velocity field will be more involved. The nonlinearity in
(6.2.2) implies that we can no longer use the principle of superposition.
Whereas for solids, the deformations caused by gravity are generally
negligible and hence are ignored, gravity is the main driving force for a
fluid. A familiar example is the flow of a fluid in a river. Note that
equations governing the deformations of a solid were expressed in terms of
displacements, those for a fluid are written in terms of velocities.
in terms of the spatial
gradients of the velocity field will be more involved. The nonlinearity in
(6.2.2) implies that we can no longer use the principle of superposition.
Whereas for solids, the deformations caused by gravity are generally
negligible and hence are ignored, gravity is the main driving force for a
fluid. A familiar example is the flow of a fluid in a river. Note that
equations governing the deformations of a solid were expressed in terms of
displacements, those for a fluid are written in terms of velocities.
For an incompressible Navier-Stokes fluid, equations expressing the balance of
mass and the balance of linear momentum are
| |
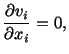 |
(6.2.3) |
| |
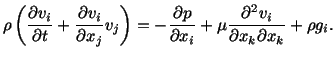 |
(6.2.4) |
The mass density 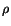 is a constant, and the pressure field
is a constant, and the pressure field 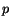 is an arbitrary function of
is an arbitrary function of
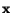 and time
and time 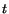 .
.
Equations (6.2.1) and (6.2.2) for a compressible Navier-Stokes fluid or
(6.2.3) and (6.2.4) for an incompressible Navier-Stokes fluid are supplemented
by the following initial and boundary conditions.
Here 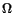 is the domain of study which may equal only a part
of the region occupied by the fluid. Equations (6.2.5) specifying the mass
density and the velocity at time
is the domain of study which may equal only a part
of the region occupied by the fluid. Equations (6.2.5) specifying the mass
density and the velocity at time 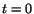 are the initial conditions, and (6.2.6)
prescribing surface tractions on a part of the boundary and velocities on the
remainder of the boundary are boundary conditions. If the velocity field is
prescribed on the entire boundary, then for an incompressible fluid, the
pressure field is indeterminate.
are the initial conditions, and (6.2.6)
prescribing surface tractions on a part of the boundary and velocities on the
remainder of the boundary are boundary conditions. If the velocity field is
prescribed on the entire boundary, then for an incompressible fluid, the
pressure field is indeterminate.
For a steady flow, the field variables 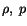 and
and
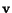 in
the spatial description are independent of time
in
the spatial description are independent of time 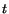 . Thus
. Thus
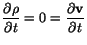 in equations (6.2.1) through (6.2.4),
and initial conditions (6.2.5) are not required.
in equations (6.2.1) through (6.2.4),
and initial conditions (6.2.5) are not required.
A flow is called irrotational if the spin tensor or the vorticity
vanishes everywhere in the domain. Governing equations for the steady
irrotational
flow of an incompressible Navier-Stokes fluid are
In writing (6.2.8) we have absorbed the constant
mass density in 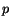 . Thus
the viscosity of a fluid does not influence the steady
irrotational flow of an
incompressible Navier-Stokes fluid.
. Thus
the viscosity of a fluid does not influence the steady
irrotational flow of an
incompressible Navier-Stokes fluid.
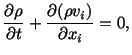
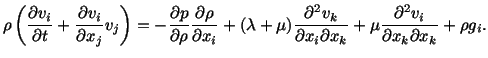
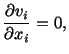
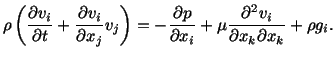
![]() and
and
![]() in
the spatial description are independent of time
in
the spatial description are independent of time ![]() . Thus
. Thus
![]() in equations (6.2.1) through (6.2.4),
and initial conditions (6.2.5) are not required.
in equations (6.2.1) through (6.2.4),
and initial conditions (6.2.5) are not required.