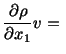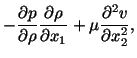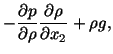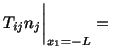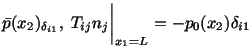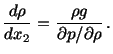Consider the steady flow of a compressible Navier-Stokes fluid between two
parallel horizontal plates with the lower plate kept stationary and the upper
one moved in the positive 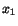 -direction at a uniform speed of
-direction at a uniform speed of 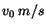 .
Assume that the fluid sticks to the plates and that
.
Assume that the fluid sticks to the plates and that
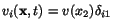 where the
where the 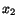 -axis is perpendicular to the plate
surfaces, and the fluid extends to infinity in the
-axis is perpendicular to the plate
surfaces, and the fluid extends to infinity in the 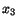 -direction. Thus we
have a two-dimensional problem in the
-direction. Thus we
have a two-dimensional problem in the 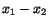 plane with the fluid flowing
only in the
plane with the fluid flowing
only in the 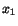 -direction. It is therefore reasonable to assume that the
mass density and the pressure field also depend only upon
-direction. It is therefore reasonable to assume that the
mass density and the pressure field also depend only upon 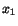 and
and 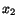 .
For the presumed velocity field,
.
For the presumed velocity field, 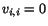 . Thus the motion is isochoric
and the mass density of a material particle does not change. Also, both the
local and the convective parts of the acceleration identically vanish.
. Thus the motion is isochoric
and the mass density of a material particle does not change. Also, both the
local and the convective parts of the acceleration identically vanish.
Nontrivial equations governing the flow of the fluid are
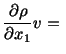 |
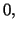 |
(6.3.1) |
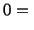 |
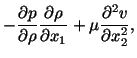 |
(6.3.2) |
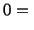 |
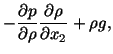 |
(6.3.3) |
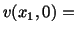 |
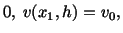 |
(6.3.4) |
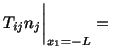 |
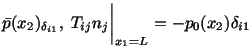 |
(6.3.5) |
Whereas equation (6.3.1) expresses the balance of mass, equations
(6.3.2) and (6.3.3) are the reduced forms of the balance of linear momentum
in the 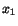 and
and 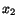 directions. Equation (6.3.4) states the essential
boundary conditions on the surfaces of the two plates, and equation (6.3.5)
gives natural boundary conditions on the vertical surfaces
directions. Equation (6.3.4) states the essential
boundary conditions on the surfaces of the two plates, and equation (6.3.5)
gives natural boundary conditions on the vertical surfaces
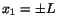 . It
follows from (6.3.1) that
. It
follows from (6.3.1) that
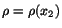 . Equations (6.3.2) and (6.3.4)
give
. Equations (6.3.2) and (6.3.4)
give
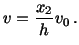 |
(6.3.6) |
Thus the velocity field is known. It follows from (6.3.3) that
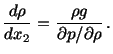 |
(6.3.7) |
The determination of 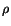 as a function of
as a function of 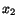 requires
that the compressibility of the fluid be known. Said differently, the
constitutive equation
requires
that the compressibility of the fluid be known. Said differently, the
constitutive equation
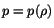 must be given. As an example, we take
must be given. As an example, we take
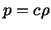 |
(6.3.8) |
where 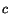 is a constant. Then, equations (6.3.7) and (6.3.8) yield
is a constant. Then, equations (6.3.7) and (6.3.8) yield
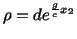 |
(6.3.9) |
where 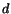 is a constant. Equations (6.3.8) and (6.3.9) imply
that
is a constant. Equations (6.3.8) and (6.3.9) imply
that 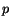 can depend only on
can depend only on 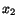 . The stress tensor in the fluid computed
from equations (6.1.3), (6.3.6), (6.3.8) and (6.3.9) is given by
. The stress tensor in the fluid computed
from equations (6.1.3), (6.3.6), (6.3.8) and (6.3.9) is given by
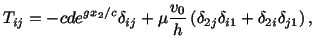 |
(6.3.10) |
and is only a function
of 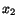 . Thus
. Thus
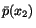 must equal
must equal 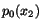 in equation (6.3.5);
otherwise there is no solution for the problem. That is, the pressure
distribution must be same on every plane
in equation (6.3.5);
otherwise there is no solution for the problem. That is, the pressure
distribution must be same on every plane
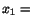 const. From equations
(6.3.5) and (6.3.10) we conclude that
const. From equations
(6.3.5) and (6.3.10) we conclude that
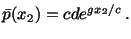 |
(6.3.11) |
That is, for the fluid being studied, surface tractions on
planes
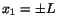 can not be arbitrarily prescribed, but must be of the
form (6.3.11). From the given value of
can not be arbitrarily prescribed, but must be of the
form (6.3.11). From the given value of
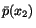 , we find the constant of
integration
, we find the constant of
integration 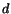 . The fields of density and velocity are respectively
given by (6.3.9) and
(6.3.6).
. The fields of density and velocity are respectively
given by (6.3.9) and
(6.3.6).
In linear elasticity, the uniquenes theorem guarantees that the solution
obtained by a semi-inverse method is the only solution of the problem.
However, in fluid mechanics, a uniqueness theorem can not be proved because of
the nonlinear governing equations. It implies that there may be other
solutions for the problem studied.
![]() -direction at a uniform speed of
-direction at a uniform speed of ![]() .
Assume that the fluid sticks to the plates and that
.
Assume that the fluid sticks to the plates and that
![]() where the
where the ![]() -axis is perpendicular to the plate
surfaces, and the fluid extends to infinity in the
-axis is perpendicular to the plate
surfaces, and the fluid extends to infinity in the ![]() -direction. Thus we
have a two-dimensional problem in the
-direction. Thus we
have a two-dimensional problem in the ![]() plane with the fluid flowing
only in the
plane with the fluid flowing
only in the ![]() -direction. It is therefore reasonable to assume that the
mass density and the pressure field also depend only upon
-direction. It is therefore reasonable to assume that the
mass density and the pressure field also depend only upon ![]() and
and ![]() .
For the presumed velocity field,
.
For the presumed velocity field, ![]() . Thus the motion is isochoric
and the mass density of a material particle does not change. Also, both the
local and the convective parts of the acceleration identically vanish.
. Thus the motion is isochoric
and the mass density of a material particle does not change. Also, both the
local and the convective parts of the acceleration identically vanish.