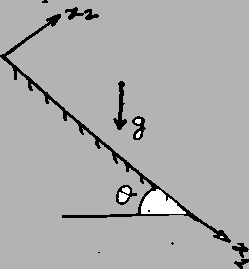
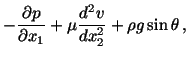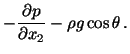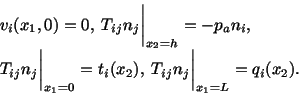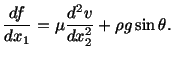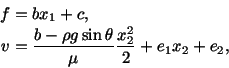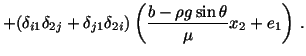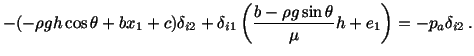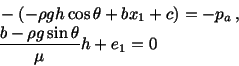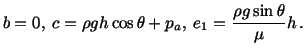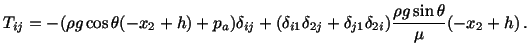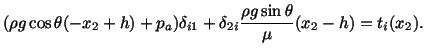In order to study this problem, it is more convenient to choose coordinate
axes with 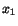 -axis along the inclined plane and
-axis along the inclined plane and 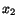 -axis perpendicular to
it. We assume that the pressure and velocity fields are independent of
-axis perpendicular to
it. We assume that the pressure and velocity fields are independent of 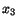 ,
and
,
and
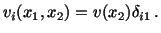 |
(6.3.12) |
That is, the fluid is flowing parallel to the inclined plane.
Thus, the top surface of the fluid will be parallel to the inclined plane.
Such a flow is called laminar.
The balance of mass or the continuity equation,
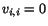 , is identically
satisfied. Also, the convective part of acceleration,
, is identically
satisfied. Also, the convective part of acceleration,
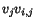 , vanishes.
Thus equations expressing the balance of linear momentum are
, vanishes.
Thus equations expressing the balance of linear momentum are
The associated boundary conditions are
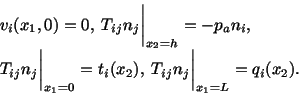 |
(6.3.15) |
That is, the fluid adheres to the
stationary inclined plane, and the surface tractions are prescribed on the top
surface and two arbitrarily chosen surfaces 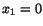 and
and 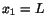 .
.
A solution of equation (6.3.14) is
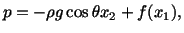 |
(6.3.16) |
where 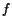 is an arbitrary smooth function of
is an arbitrary smooth function of 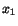 .
Substitution of (6.3.16) into (6.3.13) gives
.
Substitution of (6.3.16) into (6.3.13) gives
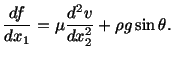 |
(6.3.17) |
Since the left-hand side of (6.3.17) is a function of 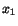 and
the right-hand side a function of
and
the right-hand side a function of 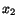 , therefore each must equal a constant
, therefore each must equal a constant
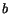 . Thus
. Thus
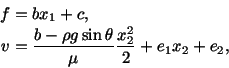 |
(6.3.18) |
where 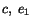 and
and 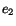 are
constants of integration. Boundary condition (6.3.15)
are
constants of integration. Boundary condition (6.3.15) requires that
requires that 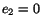 . Substitution from (6.3.12), (6.3.18) and (6.3.16) into the constitutive
relation (6.1.9) gives
. Substitution from (6.3.12), (6.3.18) and (6.3.16) into the constitutive
relation (6.1.9) gives
Equations (6.3.15)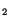 and (6.3.19) yield
and (6.3.19) yield
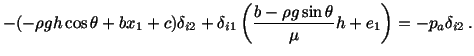 |
(6.3.20) |
Hence
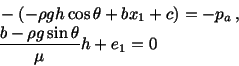 |
(6.3.21) |
Because (6.3.21)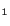 must hold for all values of
must hold for all values of 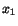 , therefore
, therefore
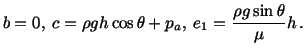 |
(6.3.22) |
With these values of 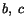 and
and 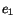 , equation (6.3.19) gives
, equation (6.3.19) gives
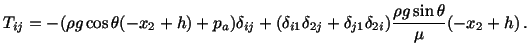 |
(6.3.23) |
Noting that on the surface
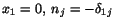 ,
equations (6.3.23) and (6.3.15) give
,
equations (6.3.23) and (6.3.15) give
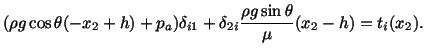 |
(6.3.24) |
One can similarly find that
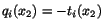 . Unless
normal and tangential tractions given by (6.3.24) are supplied on the planes
. Unless
normal and tangential tractions given by (6.3.24) are supplied on the planes
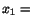 const.,
the assumed flow
const.,
the assumed flow
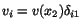 can not be
maintained on the inclined plane. The inclined plane is usually assumed to be
infinitely long and tractions necessary to maintain the flow are presumed to
act on the planes
can not be
maintained on the inclined plane. The inclined plane is usually assumed to be
infinitely long and tractions necessary to maintain the flow are presumed to
act on the planes
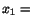 const.
const.
![]() -axis along the inclined plane and
-axis along the inclined plane and ![]() -axis perpendicular to
it. We assume that the pressure and velocity fields are independent of
-axis perpendicular to
it. We assume that the pressure and velocity fields are independent of ![]() ,
and
,
and
![]() , is identically
satisfied. Also, the convective part of acceleration,
, is identically
satisfied. Also, the convective part of acceleration,
![]() , vanishes.
Thus equations expressing the balance of linear momentum are
, vanishes.
Thus equations expressing the balance of linear momentum are