Next: Free Indices Up: Mathematical Preliminaries Previous: Mathematical Preliminaries
Consider the sum
| (2.1.1) |
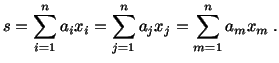 |
(2.1.2) |
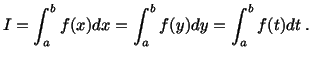 |
Using the summation convention, eqn. (2.1.2) shortens to
![]() .
.
Note that expressions such as ![]() are not defined within this
convention. That is, an index should never be repeated more than once
in the same term for the summation convention to be used. Therefore, an
expression of the form
are not defined within this
convention. That is, an index should never be repeated more than once
in the same term for the summation convention to be used. Therefore, an
expression of the form
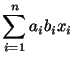 |
In the following, unless otherwise specified, we shall always take ![]() to be 3
so that, for example,
to be 3
so that, for example,
The summation convention can obviously be used to express a double sum, a triple sum, etc. For example, we can write
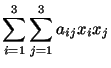 |
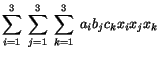 will simply be written as
will simply be written as
We emphasize again that expressions such as
![]() or
or
![]() are not defined in the summation convention.
are not defined in the summation convention.
Exercise: Given
![$\displaystyle [a_{ij}] = \left[\begin{array}{ccc}1 & 0 & 2\\ 0 & 1 & 2\\ 3 & 0 & 3\end{array}\right].$](img31.gif) |