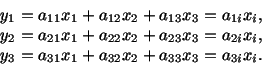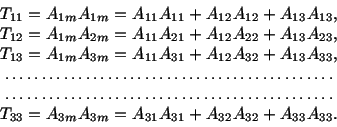Free Indices

Consider the following system of three equations:

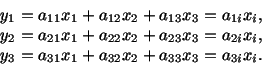$$\begin{split}&y_1 = a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = a_{1i... ..._3 = a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = a_{3i}x_i. \end{split}$$ (2.2.1)

These can be shortened to

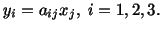$$y_i = a_{ij}x_j,\ i = 1,2,3.$$ (2.2.2)

An index which appears only once in each term of an equation such as the index 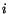$i$ in eqn. (2.2.2) is called a ``free index''. A free index takes on the integral number 1,2, or 3 one at a time. Thus eqn. (2.2.2) is a short way of writing three equations each having the sum of three terms on its right-hand side.

Note that the free index appearing in every term of an equation must be the same. Thus

$$a_i = b_j$$

is a meaningless equation. However, the following equations are meaningful.

$$\begin{split}&a_i + k_i = c_i,\\ &a_i + b_ic_jd_j = 0.\end{split}$$

If there are two free indices appearing in an equation such as

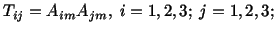$$T_{ij} = A_{im} A_{jm},\ i = 1,2,3;\ j = 1,2,3;$$ (2.2.3)

then it is a short way of writing 9 equations. For example, eqn. (2.2.3) represents 9 equations; each one has the sum of 3 terms on the right-hand side. In fact

$$\begin{array}{l} T_{11} = A_{1m}A_{1m} = A_{11} A_{11} + A_{1... ...3m} = A_{31}A_{31} + A_{32} A_{32} + A_{33} A_{33}. \end{array}$$

Again, equations such as

$$T_{ij} = T_{jk},\ T_{i\ell} = A_{im}A_{\ell\ell}$$

are meaningless.