Linear Elastic Laminate Analysis Problem: NPIB
Submit batch job to compute stresses in a thin [0/90/45/-45]s "Type-II"
Graphite/Epoxy laminated composite plate
Instructions for using this form:
- Enter appropriate numbers in the boxes,
- enter your email address,
- click on submit, and
- wait for results to be returned to your email.
(this will take about 10 seconds)
- Web location of results: lelpa.out
file will be sent to your email address.
- If your email does not provide direct email links, copy and paste the
web address: http://www.jwave.vt.edu/output/lelpat2_"unique
date-time"/lelpa.html from the email into your web browser
Location: window and look at this file to see if the job ran correctly.
- If the job ran correctly you can now download files from your
web browser to your computer for archiving (a 4.6Gbyte read/write optical
disk is available for each student to use in the SMVC for archiving large
simulation files).
- If you submit the form "as-is", a sample of results has been archived in the directory:
http://www.jwave.rkriz.net/output/ARCHIVE_Examples_SAVE/lelpat2_10-23-2000-8:37:10:645
Select
lelpat2.html to see a summary of the results.
- Results of this 2D stress calculations are compared with the 3D stresses predicted by
module09 and
module10.
- The figure below begins to define terms used in Linear Elastic Laminate Plate Analysis
(LELPA) problem and the "Free-Edge Problem". LELPA uses the Kirchoff approximation for
thin plates hence all stress associated with the z-direction are neglected. To put it
simply, LELPA analysis can only predict stresses and strains within the x-y plane of
each layer far from the free edge, whereas the Free-Edge Problem calculates the full
three-dimensional state of stress as the differential stress element, shown in the figure
below, approaches the Free-Edge.
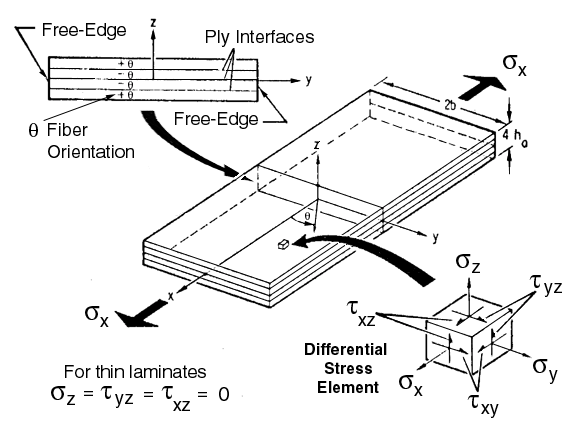
- Although the LELPA problem assumes all stresses in the z-direction are
zero, a simplified model approximates the normal stress in the z-direction.
The other shear stresses in the xz and yz planes are not calculated.
- At present the form can be used by students who are already familar with
laminated plate theory. For those already familar with with laminated plate analysis
the form and output of results should be usable. Background information is
provided that will introduce the student to
thin laminated plate analysis.

