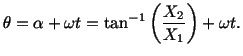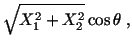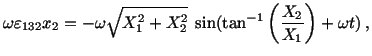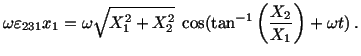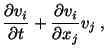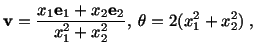The acceleration of a material particle is the rate of change of
its velocity. If the motion of a continuum is given by
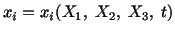 with with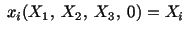 |
|
then the velocity
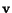 , at time
, at time 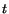 , of a particle
, of a particle 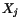 is given by
is given by
and the acceleration
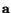 , at time
, at time 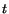 , of a particle
, of a particle
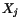 is given by
is given by
Thus, if the material description of velocity
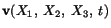 is known, then the acceleration is computed simply by taking
the partial derivative with respect to time of the function
is known, then the acceleration is computed simply by taking
the partial derivative with respect to time of the function
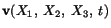 . On the other hand, if only the spatial description of
velocity (i.e.
. On the other hand, if only the spatial description of
velocity (i.e.
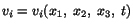 ) is known, then
the computation of acceleration involves the use of eqn. (3.5.2). That is,
) is known, then
the computation of acceleration involves the use of eqn. (3.5.2). That is,
The part of acceleration given by
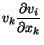 is called convective acceleration. When the motion is only along
is called convective acceleration. When the motion is only along
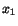 -axis, i.e.
-axis, i.e.
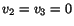 and
and
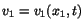 , then
, then
Example: A fluid rotates as a rigid body with a constant
angular velocity
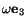 .
.
- (a)
- Write out explicitly the components of the velocity
of a material particle in the Lagrangian and Eulerian
descriptions of motion.
- (b)
- Compute the acceleration field in the Eulerian description.
Solution:
- (a)
- Recall that
Thus
is the Eulerian description of velocity.
To convert these expressions into the Lagrangian description, let the fluid
particle which presently is at place  be at place
be at place 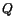 at
at 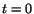 . Then,
referring to Fig. 3.6.1,
. Then,
referring to Fig. 3.6.1,
Since
- (b)
-
Exercise: Given
determine the acceleration and the rate of change of temperature
of the material particle which currently is at the place 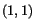 .
.
Exercise: For the motion
find the velocity and acceleration in referential and spatial descriptions.
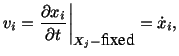
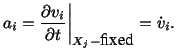

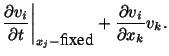
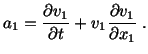
![]() .
.
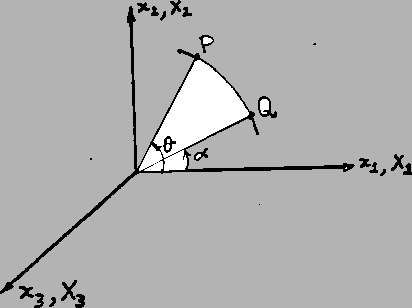
![]() be at place
be at place ![]() at
at ![]() . Then,
referring to Fig. 3.6.1,
. Then,
referring to Fig. 3.6.1,