As pointed out earlier, in
continuum mechanics, two different material particles always occupy two
distinct
places. Consider two material particles 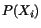 and
and
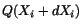 .
.
Here 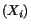 stands for the triplet
stands for the triplet
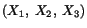 used to identify
particles in the reference configuration. Let points
used to identify
particles in the reference configuration. Let points
 and
and 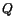 move to
move to 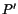 and
and 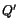 respectively so that the vector
respectively so that the vector
 is
deformed into the vector
is
deformed into the vector
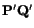 . The vector
. The vector
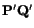 need not, and in general will not,
equal
need not, and in general will not,
equal
 . This means that the length and direction of
. This means that the length and direction of
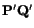 may be different from that of
may be different from that of
 . Given
. Given
 or
or
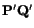 and the motion, our problem is to find
the other vector.
and the motion, our problem is to find
the other vector.
Let the motion of the body be given by
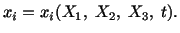 |
(3.7.1) |
Then
![$\displaystyle \mathbf{P}^\prime\mathbf{Q}^\prime = [x_i (X_1 + dX_1,X_2 + dX_2,X_3 + dX_3,t) - x_i (X_1,X_2,X_3,t)]\mathbf{e}_i.$](img516.gif) |
(3.7.2) |
Using Taylor's theorem for series expansion, we get
If points  and
and 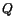 are close together in the reference
configuration, then higher order terms can be neglected as compared to terms
linear in
are close together in the reference
configuration, then higher order terms can be neglected as compared to terms
linear in 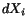 . Using this approximation, we get
. Using this approximation, we get
![$\displaystyle \mathbf{P}^\prime\mathbf{Q}^\prime = \left[\frac{\partial x_i}{\partial X_j}\bigg\vert _P dX_j\right]\mathbf{e}_i.$](img521.gif) |
(3.7.5) |
Here the suffix 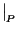 reminds us that
reminds us that
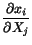 is evaluated at the
point
is evaluated at the
point  . In section 2.9, it was mentioned that a comma followed by an index
. In section 2.9, it was mentioned that a comma followed by an index
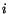 will be used to indicate partial differentiation with respect to
will be used to indicate partial differentiation with respect to 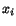 .
Now if we were to use that notation, then it will not be clear whether the
partial differentiation is with respect to
.
Now if we were to use that notation, then it will not be clear whether the
partial differentiation is with respect to 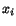 or
or 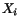 . To clarify the
situation we will, henceforth, use upper case latin indices for
. To clarify the
situation we will, henceforth, use upper case latin indices for 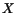 . That is,
the triplet
. That is,
the triplet
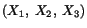 will be denoted by
will be denoted by 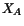 instead of
instead of 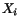 and
eqn. (3.7.5) will be written as
and
eqn. (3.7.5) will be written as
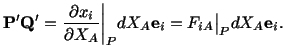 |
(3.7.6) |
In component form,
Thus 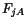 relates the components of vector
relates the components of vector
 in the reference configuration to the components of the
vector
in the reference configuration to the components of the
vector
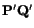 into which
into which
 is deformed. Since in Continuum Mechanics we assume that
is deformed. Since in Continuum Mechanics we assume that
therefore, 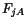 is an invertible matrix. This implies that
once the motion (3.7.1) is known, we can find
is an invertible matrix. This implies that
once the motion (3.7.1) is known, we can find
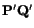 from
from
 and
vice-a-versa.
and
vice-a-versa.
Since the motion (3.7.1) gives how the body deforms and 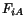 is the
gradient of the motion,
is the
gradient of the motion, 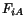 is called deformation gradient.
is called deformation gradient.
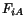 relates a vector
relates a vector
 in the reference
configuration to the vector
in the reference
configuration to the vector
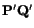 (in the
present configuration) into which
(in the
present configuration) into which
 is deformed. In
terms of the displacement
is deformed. In
terms of the displacement
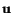 ,
, 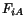 can be written as follows.
can be written as follows.
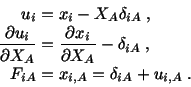 |
(3.7.8) |
The gradient 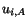 of the displacement
of the displacement
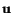 is known
as the displacement gradient.
is known
as the displacement gradient.
Example: The deformation of a body is given by
Compute the vector into which the vector
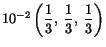 passing through the point
passing through the point 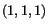 in the reference configuration is deformed.
in the reference configuration is deformed.
Solution
Here the point
 is
is 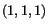 and the vector
and the vector
 has components
has components
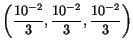 . The deformation gradient at any point is given by
. The deformation gradient at any point is given by
The deformation gradient evaluated at point  is
is
Therefore, the components of the vector
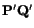 are given by
are given by
Note that, in the preceding example, the vector
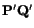 is neither parallel to
is neither parallel to
 nor is it equal to
nor is it equal to
 in magnitude.
The ratio of the length of
in magnitude.
The ratio of the length of
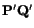 to that of
to that of
 is called stretch in the direction of
is called stretch in the direction of
 .
.
It is emphasized that in going from (3.7.4) to (3.7.5) we assumed that
the length of the vector
 is infinitesimal.
However, no assumption was made as to the magnitude1 of
is infinitesimal.
However, no assumption was made as to the magnitude1 of 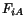 .
Thus (3.7.5) is valid no matter how large or small the components of
deformation gradient are. Said differently (3.7.5) is valid both for
small and large deformations so long as we study the deformation
of infinitesimal vectors passing through the point
.
Thus (3.7.5) is valid no matter how large or small the components of
deformation gradient are. Said differently (3.7.5) is valid both for
small and large deformations so long as we study the deformation
of infinitesimal vectors passing through the point  . Thus
. Thus 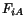 describes the deformation of material particles in an infinitesimal
neighborhood of
describes the deformation of material particles in an infinitesimal
neighborhood of  .
.
A special case in which (3.7.5) follows exactly from (3.7.4) is that when
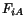 is constant. That is, each of the nine quantities
is constant. That is, each of the nine quantities
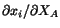 is a constant. A deformation for which
is a constant. A deformation for which 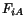 is a
constant is called a homogeneous deformation.
is a
constant is called a homogeneous deformation.
Example: Given the following displacement components
- a)
- Is this deformation possible in a continuously
deformable body? Prove your answer.
- b)
- Find the deformed vectors of the material vectors
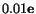 ,
and
,
and
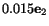 which pass through the point
which pass through the point
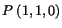 in the
reference configuration.
in the
reference configuration.
- c)
- Determine the stretches at the point
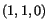 in the
in the 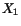 and
and
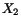 directions.
directions.
- d)
- Determine the change in angle between lines through the point
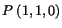 that were parallel to
that were parallel to 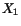 and
and 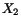 axes.
axes.
Solution:
- a)
-
Therefore, the given deformation is possible in a continuously
deformable body.
- b)
- The material vector
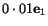 through the
material point
through the
material point 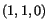 is deformed into the vector given by
is deformed into the vector given by
and
the material vector
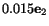 through the material point
through the material point 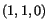 is
deformed into
is
deformed into
- c)
- Stretch at
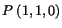 in
in
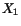 -direction
-direction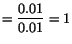 .
.
Stretch at 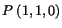 in
in
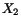 -direction
-direction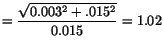 .
.
- d)
- Angle between the vectors
into which vectors
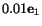 and
and
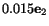 through the point
through the point 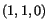 are deformed
are deformed
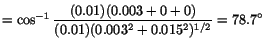 .
.
Change in angle
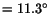 .
.
Example: Given the following displacement components
and that for points in the body,
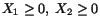 .
.
- a)
- Find the vector in the reference configuration that
ends up parallel to
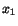 -axis through the point
-axis through the point 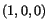 in the current
configuration.
in the current
configuration.
- b)
- Find stretch of a line element that ends up parallel to
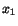 -axis
through the point
-axis
through the point 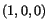 in the present configuration.
in the present configuration.
Solution: For the given displacement components,
Therefore the undeformed position of point 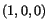 is obtained by solving
is obtained by solving
The solution of these equations which satisfies 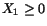 is
is
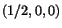 . The material particle which currently is at
. The material particle which currently is at
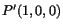 was at
was at
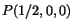 in the reference configuration.
in the reference configuration.
where
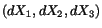 is the vector in the reference
configuration that ends up into a vector
is the vector in the reference
configuration that ends up into a vector 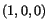 through the point
through the point 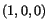 in the current configuration.
in the current configuration.
Thus a vector parallel to 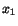 -axis through
-axis through 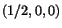 in the
reference configuration ends up into a vector parallel to
in the
reference configuration ends up into a vector parallel to 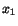 -axis through
-axis through
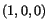 in the current configuration.
in the current configuration.
- b)
- Stretch along the desired line
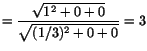 .
.
Exercise: Given the displacement field
Find the stretches and the change of angle for the material
lines 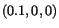 and
and 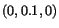 that emanate from the material particle
that emanate from the material particle
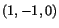 .
.
Exercise: The displacement components for a body are
- a)
- Verify that this displacement vector is
possible for a continuously deformed body.
- b)
- Is this deformation homogeneous?
- c)
- Determine the stretch in the direction
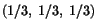 through
the point
through
the point 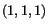 in the reference configuration.
in the reference configuration.
- d)
- Determine the direction cosines of the line element in the reference
configuration that ends up in the
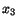 -direction at the place
-direction at the place 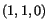 .
.
- e)
- Determine the change in angle between the lines through the point
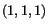 (in the reference configuration) whose directions in the reference
configuration are
(in the reference configuration) whose directions in the reference
configuration are 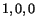 and
and
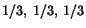 .
.
![]() and
and
![]() .
.
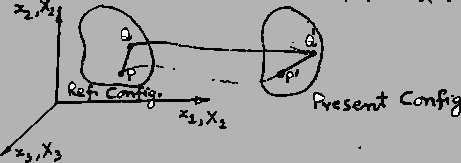
![]() stands for the triplet
stands for the triplet
![]() used to identify
particles in the reference configuration. Let points
used to identify
particles in the reference configuration. Let points
![]() and
and ![]() move to
move to ![]() and
and ![]() respectively so that the vector
respectively so that the vector
![]() is
deformed into the vector
is
deformed into the vector
![]() . The vector
. The vector
![]() need not, and in general will not,
equal
need not, and in general will not,
equal
![]() . This means that the length and direction of
. This means that the length and direction of
![]() may be different from that of
may be different from that of
![]() . Given
. Given
![]() or
or
![]() and the motion, our problem is to find
the other vector.
and the motion, our problem is to find
the other vector.
![$\displaystyle \left[\frac{\partial x_i}{\partial X_1} dX_1 + \frac{\partial x_i...
...rac{\partial x_i}{\partial X_3} dX_3\right] \mathbf{e}_i + O (\vert dX\vert^2),$](img518.gif)
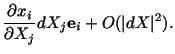
![$\displaystyle \mathbf{P}^\prime\mathbf{Q}^\prime = \left[\frac{\partial x_i}{\partial X_j}\bigg\vert _P dX_j\right]\mathbf{e}_i.$](img521.gif)
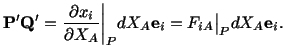
![]() is the
gradient of the motion,
is the
gradient of the motion, ![]() is called deformation gradient.
is called deformation gradient.
![]() relates a vector
relates a vector
![]() in the reference
configuration to the vector
in the reference
configuration to the vector
![]() (in the
present configuration) into which
(in the
present configuration) into which
![]() is deformed. In
terms of the displacement
is deformed. In
terms of the displacement
![]() ,
, ![]() can be written as follows.
can be written as follows.
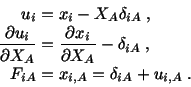
![]() is
is ![]() and the vector
and the vector
![]() has components
has components
![]() . The deformation gradient at any point is given by
. The deformation gradient at any point is given by
![$\displaystyle \left[F_{iA}\right] =\left[\begin{array}{ccc}1 + 6X_1 & 1 & 0\\ 0 & 1 + 4X_2 & 1\\ 1 & 0 & 1 + 8X_3\end{array}\right]\ .$](img539.gif)
![$\displaystyle \left[F_{iA}\right]\big\vert _P = \left[\begin{array}{ccc} 7 & 1 & 0\\ 0 & 5 & 1\\ 1 & 0 & 9\end{array}\right]\ .$](img540.gif)
![\begin{equation*}\left[\begin{array}{c} (P^\prime Q^\prime )_1\\ \noalign{\vski...
...ign{\vskip .1in} 6\\ \noalign{\vskip .1in} 10\end{array}\right].\end{equation*}](img541.gif)
![]() is neither parallel to
is neither parallel to
![]() nor is it equal to
nor is it equal to
![]() in magnitude.
The ratio of the length of
in magnitude.
The ratio of the length of
![]() to that of
to that of
![]() is called stretch in the direction of
is called stretch in the direction of
![]() .
.
![]() is infinitesimal.
However, no assumption was made as to the magnitude1 of
is infinitesimal.
However, no assumption was made as to the magnitude1 of ![]() .
Thus (3.7.5) is valid no matter how large or small the components of
deformation gradient are. Said differently (3.7.5) is valid both for
small and large deformations so long as we study the deformation
of infinitesimal vectors passing through the point
.
Thus (3.7.5) is valid no matter how large or small the components of
deformation gradient are. Said differently (3.7.5) is valid both for
small and large deformations so long as we study the deformation
of infinitesimal vectors passing through the point ![]() . Thus
. Thus ![]() describes the deformation of material particles in an infinitesimal
neighborhood of
describes the deformation of material particles in an infinitesimal
neighborhood of ![]() .
.
![]() is constant. That is, each of the nine quantities
is constant. That is, each of the nine quantities
![]() is a constant. A deformation for which
is a constant. A deformation for which ![]() is a
constant is called a homogeneous deformation.
is a
constant is called a homogeneous deformation.
![$\displaystyle \left[\begin{array}{ccc}1 & 0.2X_2 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right]$](img552.gif)
![$\displaystyle \left[\begin{array}{ccc} 1 & 0.2(1) & 0\\ 0 & 1 & 0\\ 0 & 0 & 1...
...\end{array}\right] = \left[\begin{array}{c} 0.01\\ 0\\ 0\end{array}\right]\ ,$](img556.gif)
![$\displaystyle \left[\begin{array}{ccc} 1 & 0.2(1) & 0\\ 0 & 1 & 0\\ 0 & 0 & 1...
...array}\right] = \left[\begin{array}{c} 0.003\\ 0.015\\ 0\end{array}\right]\ .$](img557.gif)
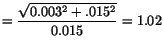 .
.
![$\displaystyle \left[\begin{array}{ccc} 1+4X_1+X_2 & X_1 & 0\\ 0 & 1 + 2X_2 & 0\\ 0 & 0 & 1\end{array}\right]$](img576.gif)
![$\displaystyle \left[\begin{array}{ccc} 3 & 0.5 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right]$](img578.gif)
![% latex2html id marker 12530
$\displaystyle \therefore \hspace*{.2in} \left[\begin{array}{c}1\\ 0\\ 0\end{array}\right] =\ $](img579.gif)
![$\displaystyle \left[\begin{array}{ccc} 3 & 0.5 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c} dX_1 \\ dX_2\\ dX_3\end{array}\right]$](img580.gif)
![$\displaystyle \left[\begin{array}{c} dX_1\\ dX_2\\ dX_3\end{array}\right] = 1...
... 0\end{array}\right] = \left[\begin{array}{c} 1/3\\ 0 \\ 0\end{array}\right].$](img582.gif)
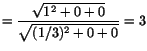 .
.