As seen in the previous section, during the motion of a deformable continuum,
material lines originating from a material point are rotated and stretched.
Whenever the material lines emanating from a material point are stretched
and/or the angle between two different material lines passing through a
material point changes, the body is said to be strained or deformed.
We have seen in the
previous section that the deformation gradient is a measure of the stretch and
rotation of various material vectors. In this section we will introduce two
more measures of deformation which, of course, will be related to the
deformation gradient.
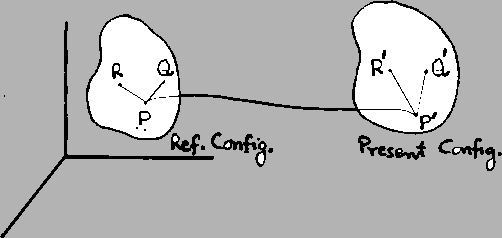
Consider two material vectors
 and
and
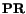 originating from the material point
originating from the material point 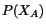 in the
reference configuration. Let
in the
reference configuration. Let
 be deformed into
be deformed into
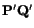 and
and
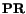 into
into
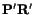 . Then
. Then
Henceforth we will drop the suffix 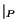 to shorten the notation.
Of course,
to shorten the notation.
Of course, 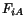 is to be evaluated at the material point
is to be evaluated at the material point  . Therefore,
. Therefore,
where
![$\displaystyle C_{AB} = F_{jA}F_{jB}\ {\rm or}\ [\mathbf{C}] = [\mathbf{F}]^T [\mathbf{F}].$](img602.gif) |
(3.8.2) |
Note that
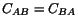 , that is the matrix
, that is the matrix
![$ [\mathbf{C}]$](img604.gif) is
symmetric. To obtain a physical interpretation of various components of
is
symmetric. To obtain a physical interpretation of various components of
![$ [\mathbf{C}]$](img604.gif) , let
, let
Then (3.8.1) gives
so that
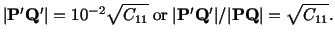 |
(3.8.3) |
Thus 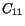 is a measure of the stretch along
is a measure of the stretch along 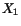 -axis.
Similarly
-axis.
Similarly 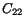 and
and 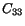 measure stretches along
measure stretches along 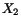 and
and 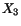 axes
respectively. Now take
axes
respectively. Now take
Then (3.8.1) gives
The left-hand side of (3.8.4) equals cosine of the angle between
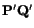 and
and
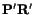 . Thus
. Thus 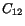 provides a measure of the
change in angle between two material lines passing through the point
provides a measure of the
change in angle between two material lines passing through the point  that in the reference configuration were parallel to
that in the reference configuration were parallel to 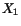 and
and 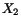 -axes.
Similarly
-axes.
Similarly 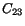 measures the change in angle
at the material point
measures the change in angle
at the material point  between two material lines that in the reference
configuration were parallel to
between two material lines that in the reference
configuration were parallel to 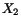 and
and 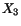 axes.
axes.
In terms of displacement components 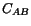 can be written as follows.
can be written as follows.
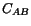 is called the right Cauchy-Green tensor. The tensor
is called the right Cauchy-Green tensor. The tensor
is known as the Green-St. Venant strain tensor. We note from (3.8.1) that
so that 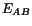 measures the change in lengths of various material
line elements and the change in angles between different material lines
emanating in the reference configuration from the same material point.
It follows from eqn. (3.8.7) that
measures the change in lengths of various material
line elements and the change in angles between different material lines
emanating in the reference configuration from the same material point.
It follows from eqn. (3.8.7) that
where
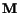 and
and
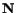 are unit vectors parallel to
are unit vectors parallel to
 and
and
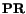 respectively.
respectively.
Since
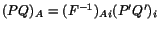 , therefore
, therefore
where
![$\displaystyle B_{ij} = F_{iA}F_{jA},\ [\mathbf{B}] = [\mathbf{F}][\mathbf{F}^T],$](img642.gif) |
(3.8.10) |
is the left Cauchy-Green tensor. The tensor
is called the Almansi-Hamel tensor. It follows from (3.8.9)
and (3.8.11) that
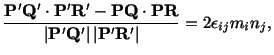 |
(3.8.12) |
where
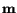 and
and
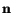 are unit vectors parallel
to
are unit vectors parallel
to
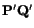 and
and
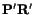 in the present configuration. It is
evident from eqn. (3.8.12) that
in the present configuration. It is
evident from eqn. (3.8.12) that
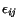 also measures changes in
lengths of line elements and changes in angles between different line
elements in the present configuration.
also measures changes in
lengths of line elements and changes in angles between different line
elements in the present configuration.
In the referential description of motion, 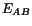 is used as a measure of
strain. However,
is used as a measure of
strain. However,
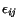 is used to measure strain in the spatial
description of motion. Note that each one of these two tensors vanishes when
there is no deformation.
is used to measure strain in the spatial
description of motion. Note that each one of these two tensors vanishes when
there is no deformation.
Exercise: By taking
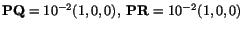 , and using (3.8.7),
prove that
, and using (3.8.7),
prove that
Hence find the engineering strain (elongation/original length)
along  -axis.
-axis.
Exercise: By setting
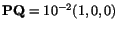 and
and
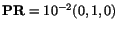 into (3.8.7), and
using the result of the previous exercise, obtain an expression for the cosine
of the angle between
into (3.8.7), and
using the result of the previous exercise, obtain an expression for the cosine
of the angle between
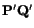 and
and
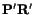 .
.
![]() and
and
![]() originating from the material point
originating from the material point ![]() in the
reference configuration. Let
in the
reference configuration. Let
![]() be deformed into
be deformed into
![]() and
and
![]() into
into
![]() . Then
. Then
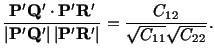
![]() can be written as follows.
can be written as follows.
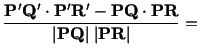
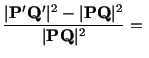
![]() , therefore
, therefore
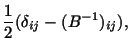
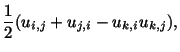
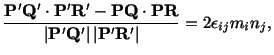
![]() is used as a measure of
strain. However,
is used as a measure of
strain. However,
![]() is used to measure strain in the spatial
description of motion. Note that each one of these two tensors vanishes when
there is no deformation.
is used to measure strain in the spatial
description of motion. Note that each one of these two tensors vanishes when
there is no deformation.
![]() , and using (3.8.7),
prove that
, and using (3.8.7),
prove that
![]() and
and
![]() into (3.8.7), and
using the result of the previous exercise, obtain an expression for the cosine
of the angle between
into (3.8.7), and
using the result of the previous exercise, obtain an expression for the cosine
of the angle between
![]() and
and
![]() .
.