Having learned how to find the deformation of various material vectors
emanating from a material point  , we now investigate which of these lines
is stretched the most. Let
, we now investigate which of these lines
is stretched the most. Let
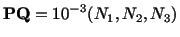 |
(3.9.1) |
where
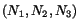 are components of a unit vector along
are components of a unit vector along
 . That is,
. That is,
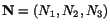 is a unit
vector along
is a unit
vector along
 . Our aim is to find
. Our aim is to find
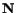 such
that the stretch at
such
that the stretch at  along
along
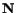 is maximum or minimum. The vector
is maximum or minimum. The vector
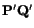 into which
into which
 is
deformed is given by
is
deformed is given by
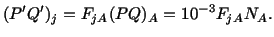 |
(3.9.2) |
Therefore,
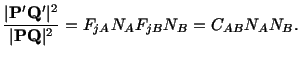 |
(3.9.3) |
Thus the problem reduces to finding a unit vector
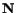 such that
such that
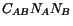 is maximum. By using the method of Lagrange
multipliers we need to find
is maximum. By using the method of Lagrange
multipliers we need to find
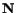 such that
such that
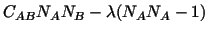 |
(3.9.4) |
takes on extreme values for all
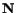 . In (3.9.4)
. In (3.9.4)
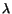 is a Lagrange multiplier. Such an
is a Lagrange multiplier. Such an
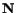 is given by
is given by
which is equivalent to
or
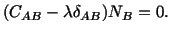 |
(3.9.5) |
These are three linear homogeneous equations in
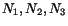 .
A non-trivial solution of these equations exists if and only if
.
A non-trivial solution of these equations exists if and only if
or
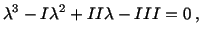 |
(3.9.6) |
where
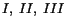 are called principal invariants of
are called principal invariants of
![$ [\mathbf{C}]$](img604.gif) .
Equation (3.9.6) is cubic in
.
Equation (3.9.6) is cubic in 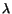 and will have three roots. Since the
matrix
and will have three roots. Since the
matrix
![$ [\mathbf{C}]$](img604.gif) is symmetric and positive definite, all three roots
of (3.9.6)
are positive. Let us denote the three roots of (3.9.6) by
is symmetric and positive definite, all three roots
of (3.9.6)
are positive. Let us denote the three roots of (3.9.6) by
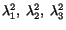 .2For each one of these roots of (3.9.6) we
find the corresponding
.2For each one of these roots of (3.9.6) we
find the corresponding
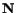 from (3.9.5). That is, once the three
roots of (3.9.6) have been found, we use (3.9.5) to find the directions
from (3.9.5). That is, once the three
roots of (3.9.6) have been found, we use (3.9.5) to find the directions
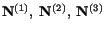 along which stretches
assume extreme values. For example,
along which stretches
assume extreme values. For example,
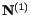 is obtained by solving
is obtained by solving
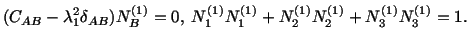 |
(3.9.7) |
Having found
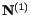 , we use (3.9.3) to find the
stretch in this direction.
, we use (3.9.3) to find the
stretch in this direction.
Thus the three roots of (3.9.6) are squares of extreme values of
stretches at the point  . Let us now assume that
. Let us now assume that
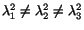 and find the angle between directions
and find the angle between directions
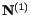 and
and
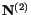 . Rewriting (3.9.7) as
. Rewriting (3.9.7) as
we obtain
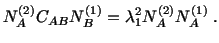 |
(3.9.8) |
Similarly
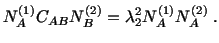 |
(3.9.9) |
Since
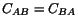 , therefore, the left-hand sides of
(3.9.8) and (3.9.9) are equal. Thus
, therefore, the left-hand sides of
(3.9.8) and (3.9.9) are equal. Thus
Since
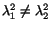 by assumption,
by assumption,
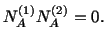 |
(3.9.10) |
Thus
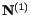 and
and
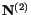 are
perpendicular to each other. By using the same argument for
are
perpendicular to each other. By using the same argument for
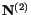 and
and
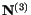 , we conclude that whenever
, we conclude that whenever
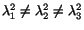 ,
,
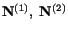 and
and
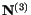 are mutually perpendicular to each
other.
are mutually perpendicular to each
other.
Let us now find the change in the angle between the lines
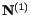 and
and
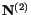 during the deformation. If
during the deformation. If 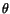 is the angle
between the deformed positions of
is the angle
between the deformed positions of
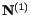 and
and
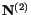 ,
then by (3.8.1) and (3.8.4)
,
then by (3.8.1) and (3.8.4)
That is, the angle between directions
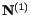 and
and
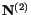 does not change during the deformation. The same holds
true for directions
does not change during the deformation. The same holds
true for directions
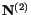 and
and
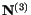 . Because of
this property, the directions
. Because of
this property, the directions
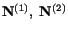 and
and
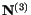 are called principal axes of stretch and
are called principal axes of stretch and
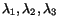 are called principal stretches.
are called principal stretches.
Whenever any two or all roots of eqn. (3.9.6) are equal, equations (3.9.10)
and (3.9.11) hold for suitable choices of
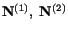 and
and
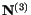 . If
. If
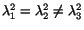 , then
, then
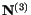 is uniquely determined but
is uniquely determined but
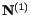 and
and
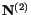 can be taken as any two directions in a plane perpendicular
to
can be taken as any two directions in a plane perpendicular
to
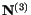 . When
. When
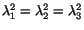 , then
any three linearly independent directions which need not be mutually
perpendicular to each other can be taken as
, then
any three linearly independent directions which need not be mutually
perpendicular to each other can be taken as
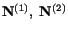 , and
, and
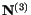 .
.
Recalling that
we obtain
To arrive at this equation, we used (3.9.7). Thus
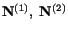 and
and
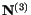 are the
directions along which
are the
directions along which
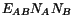 takes on extreme values
takes on extreme values
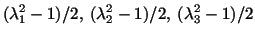 |
(3.9.13) |
respectively. If we define strain in the direction
 as
as
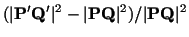 |
(3.9.14) |
instead of the engineering strain
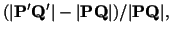 |
(3.9.15) |
we see from (3.8.7) that
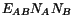 gives strain in the
direction
gives strain in the
direction
 . Thus the three numbers given by (3.9.13) are the
extreme values of strains and since the angle between the mutually orthogonal
directions
. Thus the three numbers given by (3.9.13) are the
extreme values of strains and since the angle between the mutually orthogonal
directions
 does not
change, (3.9.13) are the principal strains and
does not
change, (3.9.13) are the principal strains and
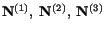 are the axes of
principal strain. Note that there is no shear strain between any two of the
three directions
are the axes of
principal strain. Note that there is no shear strain between any two of the
three directions
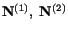 and
and
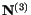 .
.
APPENDIX: SOLUTION OF A CUBIC EQUATION
The solution of a general cubic equation, which may have imaginary roots, in a
closed form involves the use of hyperbolic functions. However, the cubic
equation obtained from
![$\displaystyle \det[C_{AB} - \lambda \delta_{AB}] = 0$](img711.gif) |
(A1) |
in which
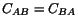 has only real roots, and
can be solved as follows.
has only real roots, and
can be solved as follows.
The cubic equation
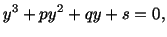 |
(A2) |
can be reduced to the form
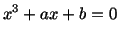 |
(A3) |
by substituting
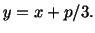 |
(A4) |
In (A3)
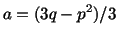 and and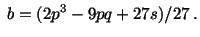 |
|
The reduced cubic equation (A3) can be solved by
transforming it to the trignometric identity
(See pages 93-95, CRC Standard Mathematical Tables). The
solution of the equation
obtained by this method is
where
Example: The deformation of a body is given by
- a)
- Find the principal strains at the material point
(1,1,1) in the reference configuration.
- b)
- Find the axis of the maximum strain through the material point
(1,1,1) in the reference configuration. Also find the direction cosines of
the line into which this axis is deformed.
Solution:
- (a)
- At any point
Thus
The principal invariants of
![$ [\mathbf{C}]$](img604.gif) are given by
are given by
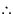 Principal strains at the material point
Principal strains at the material point 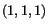 are
42.06, 23.95, 11.5.
are
42.06, 23.95, 11.5.
- (b)
- To obtain
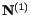 we need to solve
we need to solve
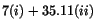 gives
gives
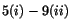 gives
gives
Substituting for 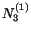 and
and 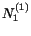 into (iv), we get
into (iv), we get
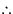 The axis of the maximum strain at the material
point
The axis of the maximum strain at the material
point
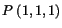 is
is
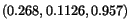 .
.
To find the direction cosines of the line into which this is deformed, let
Then
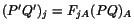 ,
,
 Direction cosines of
Direction cosines of
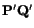 are
are
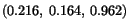 .
.
Exercise: Given the displacement components
- a)
- Find the principal strains at the material point
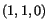 in the reference configuration.
in the reference configuration.
- b)
- Find the axis of the maximum strain at the point
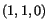 in the
reference configuration.
in the
reference configuration.
Exercise: Given the following displacement components
Find the principal strains and their axes at the material point
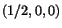 in the reference configuration.
in the reference configuration.
![]() , we now investigate which of these lines
is stretched the most. Let
, we now investigate which of these lines
is stretched the most. Let
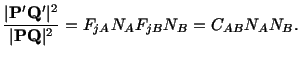
![$\displaystyle \frac{\partial}{\partial N_I}[C_{AB}N_AN_B - \lambda (N_AN_A-1)] = 0$](img662.gif)

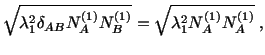
![]() and
and
![]() during the deformation. If
during the deformation. If ![]() is the angle
between the deformed positions of
is the angle
between the deformed positions of
![]() and
and
![]() ,
then by (3.8.1) and (3.8.4)
,
then by (3.8.1) and (3.8.4)
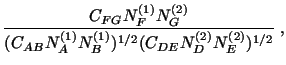
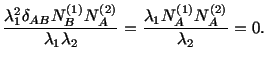
![]() and
and
![]() . If
. If
![]() , then
, then
![]() is uniquely determined but
is uniquely determined but
![]() and
and
![]() can be taken as any two directions in a plane perpendicular
to
can be taken as any two directions in a plane perpendicular
to
![]() . When
. When
![]() , then
any three linearly independent directions which need not be mutually
perpendicular to each other can be taken as
, then
any three linearly independent directions which need not be mutually
perpendicular to each other can be taken as
![]() , and
, and
![]() .
.
![$\displaystyle [F_{iA}] = \left[\begin{array}{ccc}1 + 6X_1 & 1 & 0\\ 0 & 1 + 4X_2 & 1\\ 1 & 0 & 1 + 8X_3\end{array}\right]\ .$](img725.gif)
![$\displaystyle [F_{iA}\vert _{(1,1,1)}] = \left[\begin{array}{ccc} 7 & 1 & 0\\ 0 & 5 & 1\\ 1 & 0 & 9\end{array}\right]\ ,$](img726.gif)
![$\displaystyle \left[\begin{array}{ccc} 7 & 0 & 1\\ 1 & 5 & 0\\ 0 & 1 & 9\end{ar...
...\left[\begin{array}{ccc} 7 & 1 & 0\\ 0 & 5 & 1\\ 1 & 0 & 9\end{array}\right]\ ,$](img728.gif)
![$\displaystyle \left[\begin{array}{ccc}50 & 7 & 9\\ 7 & 26 & 5\\ 9 & 5 & 82\end{array}\right]\ .$](img729.gif)
![$\displaystyle \det [\mathbf{C}] (C^{-1})_{AA} = \left\vert\begin{array}{rr}26 &...
...t + \left\vert\begin{array}{rr} 50 & 7\\ 7 & 26\end{array}\right\vert = 7377\ ,$](img732.gif)
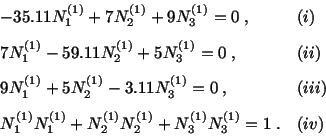
![$\displaystyle [\mathbf{P}^\prime\mathbf{Q}^\prime] = ds\left[\begin{array}{ccc}...
...ray} \right] = ds\left[\begin{array}{l}1.989\\ 1.52\\ 8.881\end{array}\right]$](img760.gif)