Next: Mass density. Equation of Up: Kinematics Previous: Principal Strains
Consider two different infinitesimal line elements
![]() and
and
![]() emanating from a point
emanating from a point ![]() in the reference
configuation. During the deformation lines
in the reference
configuation. During the deformation lines
![]() and
and
![]() are deformed into
are deformed into
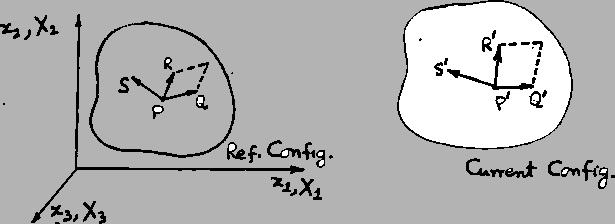
![]() and
and
![]() respectively. Hence the parallelogram whose adjacent sides are
respectively. Hence the parallelogram whose adjacent sides are
![]() and
and
![]() in the reference
configuration is deformed into the one with adjacent sides as
in the reference
configuration is deformed into the one with adjacent sides as
![]() and
and
![]() .
Let us denote the areas of these by
.
Let us denote the areas of these by
![]() and
and
![]() respectively. Then
respectively. Then
| (3.10.1) |
Now consider the parallelepiped formed by three nonplanar infinitesimal line
elements
![]() ,
,
![]() and
and
![]() passing through a point
passing through a point ![]() in the reference
configuration. Because of the deformation, the parallelepiped is deformed
into the one whose three concurrent sides are
in the reference
configuration. Because of the deformation, the parallelepiped is deformed
into the one whose three concurrent sides are
![]() ,
,
![]() and
and
![]() . If
. If ![]() and
and ![]() denote the volumes of
these in the reference and the current configurations respectively, then
denote the volumes of
these in the reference and the current configurations respectively, then
| (3.10.2) |
A deformation such that
Exercise: Given the following deformation
Exercise: The displacement components for a body are
![]() . At the material point
. At the material point ![]() on
the surface of the body in the reference configuration, an element of area has
components
on
the surface of the body in the reference configuration, an element of area has
components
![]() . Find the components of the area into which this
is deformed.
. Find the components of the area into which this
is deformed.