Consider a sphere of infinitesimal radius centered at a point  in the
reference configuration. The material contained within the sphere has mass
in the
reference configuration. The material contained within the sphere has mass
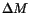 . Let
. Let 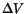 denote the volume of the sphere. The mass density
denote the volume of the sphere. The mass density
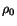 at point
at point  in the reference configuration is defined as
in the reference configuration is defined as
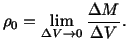 |
(3.11.1) |
One of the assumptions in continuum mechanics is that the limit
on the right-hand side of (3.11.1) exists at every point of the body. Since
both 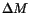 and
and 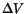 are positive, therefore, the mass density
are positive, therefore, the mass density
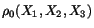 is positive. Note that from the point of view of
Atomic Physics, the assumption that the right-hand side of (3.11.1) is well
defined may not be justified. One can always envisage infinitesimal volume
elements surrounding a point which contain no atomic particles at some time
and hence will make the mass density at the point to be zero at that time.
However, in continuum mechanics, we are concerned with gross effects or
macroeffects of deformation, and lengths considered are much larger than the
distance between adjacent atoms.
is positive. Note that from the point of view of
Atomic Physics, the assumption that the right-hand side of (3.11.1) is well
defined may not be justified. One can always envisage infinitesimal volume
elements surrounding a point which contain no atomic particles at some time
and hence will make the mass density at the point to be zero at that time.
However, in continuum mechanics, we are concerned with gross effects or
macroeffects of deformation, and lengths considered are much larger than the
distance between adjacent atoms.
We now make the assumption that the mass of the material contained in every
small volume element at  is conserved. That is, the mass of the matter
enclosed in the infinitesimal parallelepiped at
is conserved. That is, the mass of the matter
enclosed in the infinitesimal parallelepiped at  equals the mass of the
matter contained in the infinitesimal parallelepiped at
equals the mass of the
matter contained in the infinitesimal parallelepiped at 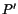 into which
the former is deformed. Denoting the mass density in the present
configuration by
into which
the former is deformed. Denoting the mass density in the present
configuration by 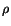 , we have
, we have
Substituting for 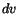 from (3.10.2), we arrive at
from (3.10.2), we arrive at
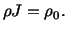 |
(3.11.2) |
or
Equation (3.11.2) which relates the mass density in the present
configuration to the mass density in the reference configuration is the
equation of continuity or the conservation of mass
in the Lagrangian description.
To obtain the equation of continuity in the spatial description, we take the
material derivative of (3.11.2) and thereby obtain
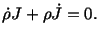 |
(3.11.3) |
Since
therefore,
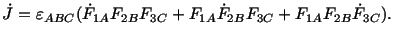 |
(3.11.4) |
However,
Similarly, one can show that
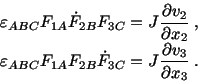 |
(3.11.6) |
Substituting from (3.11.5) and (3.11.6) into (3.11.4) and then
the result into (3.11.3) we get
and thus conclude that
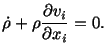 |
(3.11.7) |
This equation can equivalently be written as
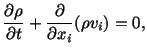 |
(3.11.8) |
which is the continuity equation in spatial description.
For an isochoric deformation
and hence
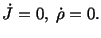 |
(3.11.9) |
Equations (3.11.9) and (3.11.7) imply that for an isochoric
deformation, the continuity equation assumes the form
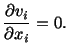 |
(3.11.10) |
Exercise: Show that
are the components of a velocity field in an isochoric deformation.
Example: For the velocity field given by
find the density of a material particle as a function of time.
Solution: For the given velocity field,
Therefore, from the conservation of mass, we get
Integration of this equation gives
where 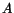 is a constant of integration. If
is a constant of integration. If
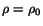 at
at 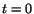 , then
, then
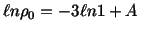 or or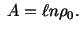 |
|
Thus eqn. 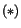 becomes
becomes
Exercise: Given the velocity field
determine how the fluid density varies with time.
Exercise: In the spatial description the density of an
incompressible fluid is given by
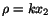 . Find a permissible form for
the velocity field, with
. Find a permissible form for
the velocity field, with  , in order that the conservation of mass
equation be satisfied.
, in order that the conservation of mass
equation be satisfied.
![]() in the
reference configuration. The material contained within the sphere has mass
in the
reference configuration. The material contained within the sphere has mass
![]() . Let
. Let ![]() denote the volume of the sphere. The mass density
denote the volume of the sphere. The mass density
![]() at point
at point ![]() in the reference configuration is defined as
in the reference configuration is defined as
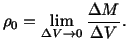
![]() is conserved. That is, the mass of the matter
enclosed in the infinitesimal parallelepiped at
is conserved. That is, the mass of the matter
enclosed in the infinitesimal parallelepiped at ![]() equals the mass of the
matter contained in the infinitesimal parallelepiped at
equals the mass of the
matter contained in the infinitesimal parallelepiped at ![]() into which
the former is deformed. Denoting the mass density in the present
configuration by
into which
the former is deformed. Denoting the mass density in the present
configuration by ![]() , we have
, we have

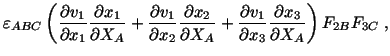
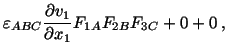
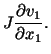
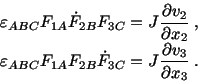
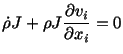
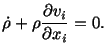
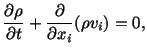
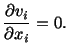
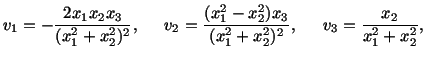
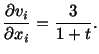
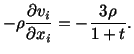
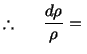
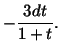
![]() . Find a permissible form for
the velocity field, with
. Find a permissible form for
the velocity field, with ![]() , in order that the conservation of mass
equation be satisfied.
, in order that the conservation of mass
equation be satisfied.