Let us consider a material element
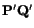 emanating from a material point located at
emanating from a material point located at
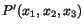 in the
present configuration at time
in the
present configuration at time 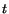 . We wish to compute
. We wish to compute
 , the rate of
change of length and direction of
, the rate of
change of length and direction of
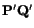 . Let
. Let
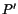 be the deformed position of the material point located at
be the deformed position of the material point located at
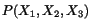 in the reference configuration and
in the reference configuration and 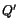 that of
that of
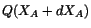 . Then
. Then
Thus,
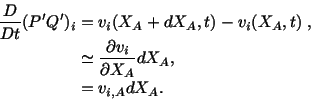 |
(3.12.1) |
Equation (3.12.1) expresses
 in a material
description. To obtain
in a material
description. To obtain
 in a spatial
description, we note that since
in a spatial
description, we note that since
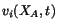 is the velocity of a material
point
is the velocity of a material
point  presently at the position
presently at the position 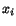 , therefore, if a spatial description
of velocity is employed, this velocity is given by
, therefore, if a spatial description
of velocity is employed, this velocity is given by
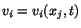 . Note
that
. Note
that
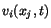 and
and
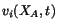 are, in general, different functions.
Thus,
are, in general, different functions.
Thus,
where we have set
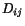 , the symmetric part of the velocity gradient
, the symmetric part of the velocity gradient 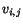 , is
known as the rate of deformation tensor or the strain-rate
tensor, and
, is
known as the rate of deformation tensor or the strain-rate
tensor, and 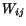 , the antisymmetric
part of the velocity gradient
, the antisymmetric
part of the velocity gradient 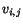 , is known as the spin tensor.
, is known as the spin tensor.
In the following, we give a geometric interpretation of the elements of
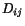 . Let
. Let
where
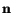 is a unit vector in the direction of
is a unit vector in the direction of
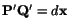 . Then
. Then
where we have substituted for
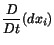 from (3.12.3). Since
from (3.12.3). Since
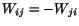 , therefore
, therefore
and we get
or
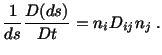 |
(3.12.6) |
If
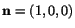 , the right-hand side of (3.12.6)
equals
, the right-hand side of (3.12.6)
equals 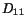 . Thus
. Thus 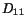 gives the rate of change of length per unit
length known as stretching or rate of extension for a material line
presently parallel to
gives the rate of change of length per unit
length known as stretching or rate of extension for a material line
presently parallel to 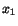 -axis. Similarly
-axis. Similarly 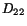 and
and 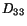 give,
respectively, the stretching of a material line presently in the
give,
respectively, the stretching of a material line presently in the
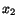 - and
- and 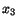 -direction. To obtain a physical interpretation of
the off-diagonal elements of
-direction. To obtain a physical interpretation of
the off-diagonal elements of 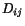 , let
, let
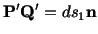 and and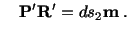 |
|
Then
| |
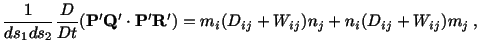 |
|
| |
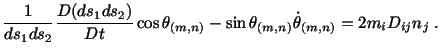 |
(3.12.7) |
Here
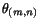 is the angle between directions
is the angle between directions
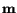 and
and
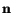 . Thus for
. Thus for
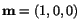 and
and
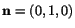 ,
the right-hand side of (3.12.7) equals
,
the right-hand side of (3.12.7) equals 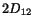 and the left-hand side equals
and the left-hand side equals
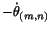 . Hence
. Hence 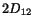 equals the rate of decrease of angle
from
equals the rate of decrease of angle
from
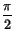 of two line elements presently parallel to
of two line elements presently parallel to
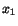 and
and 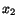 -axes, known as shearing or rate of shear. A
similar interpretation holds for
-axes, known as shearing or rate of shear. A
similar interpretation holds for 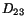 and
and 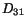 .
.
Since 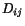 is symmetric, we also have the result that there always exist
three mutually perpendicular directions (eigenvectors of
is symmetric, we also have the result that there always exist
three mutually perpendicular directions (eigenvectors of 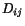 ) along which
the stretching (an eigenvalue of
) along which
the stretching (an eigenvalue of 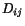 ) is either maximum or minimum
among stretchings for
all differential elements extending from the material particle which
currently is at
) is either maximum or minimum
among stretchings for
all differential elements extending from the material particle which
currently is at  .
.
Note that the strain-rate tensor does not, in general, equal the time rate of
change of the strain tensor. To prove this, we first conclude from eqns. (3.12.2) and (3.7.7) that
which must hold for all choices of 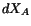 . Thus
. Thus
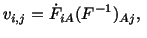 or or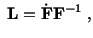 |
(3.12.8) |
where
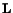 is the spatial velocity gradient.
Differentiation of both sides of (3.8.2) with respect to time and the
definition (3.8.6)
is the spatial velocity gradient.
Differentiation of both sides of (3.8.2) with respect to time and the
definition (3.8.6)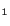 of the strain tensor
of the strain tensor
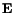 gives
gives
Hence
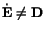 , and the strain-rate tensor
, and the strain-rate tensor
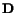 should not be confused with the time rate of change of the strain tensor
should not be confused with the time rate of change of the strain tensor
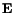 .
.
We now attempt to provide a physical interpretation of the spin tensor. Let
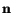 be a unit eigenvector of
be a unit eigenvector of
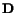 , i.e.,
, i.e.,
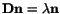 where
where 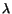 is the eigenvalue
corresponding to
is the eigenvalue
corresponding to
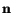 . From (3.12.3), we have
. From (3.12.3), we have
where we have used (3.12.6). It states that the spin tensor
operating on a unit eigenvector of
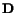 gives the rate of change of
that unit vector. Thus the spin equals the angular velocity of the principal
axes of stretching.
gives the rate of change of
that unit vector. Thus the spin equals the angular velocity of the principal
axes of stretching.
The axial vector
is the vorticity vector; its direction is the axis of
spin, and its magnitude is the vorticity magnitude, 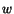 .
.
We now show that the spin tensor defined by (3.12.4)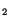 does not equal the
rate of change of the rotation matrix
does not equal the
rate of change of the rotation matrix
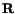 . Equations (3.12.9) and
(3.13.1)
. Equations (3.12.9) and
(3.13.1)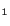 give
give
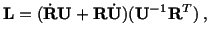 |
(3.13.15) |
or
where we have added and subtracted
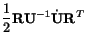 to the
right-hand side. Equating symmetric and skew-symmetric tensors on both sides,
we obtain
to the
right-hand side. Equating symmetric and skew-symmetric tensors on both sides,
we obtain
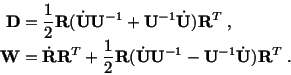 |
(3.13.17) |
These equations clearly evince that
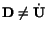 and
and
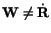 .
.
Taking the material derivative of both sides of eqn. (3.10.2) we obtain
and, therefore,
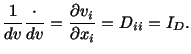 |
(3.12.13) |
In going from (3.12.11) to (3.12.12) we used
which can be obtained from eqns. (3.11.4), (3.11.5) and
(3.11.6). Thus the first principal invariant 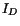 of the rate of deformation
tensor
of the rate of deformation
tensor 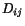 gives the rate of change of volume per unit volume.
gives the rate of change of volume per unit volume.
We now derive an expression for the rate of change of an area element.
Rewriting eqn. (3.10.1) as
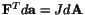 and
taking the time derivative of both sides, we obtain
and
taking the time derivative of both sides, we obtain
In an isochoric deformation,
 but
but
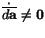 in general.
in general.
Example: Given the velocity field
find
- (a)
- the rate of deformation and the spin tensors,
- (b)
- the rate of extension per unit length of the line element
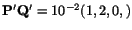 ,
,
- (c)
- the maximum and the minimum rates of extension.
Solution
- (a)
- The matrix of the velocity gradient is
Therefore,
- (b)
- Given
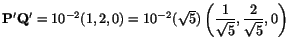 . Thus
. Thus
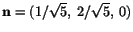 . From eqn. (3.12.6)
. From eqn. (3.12.6)
- (d)
- From the characteristic equation
we determine the eigenvalues of the tensor  as
as
 . Therefore, 1 is the maximum and
. Therefore, 1 is the maximum and 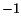 the minimum rate of
extension. The eigenvector
the minimum rate of
extension. The eigenvector
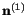 (for
(for
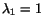 )
determined from
)
determined from
is
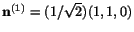 . Similarly
. Similarly
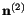 corresponding to
corresponding to
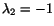 is
is
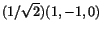 .
The third eigenvector is
.
The third eigenvector is
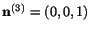 .
.
Exercise: For the velocity field
find
- a)
- the rate of extension per unit length of a
material line element which in the present configuration is given by
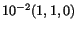 through the point
through the point 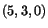 ,
,
- b)
- the deformation corresponding to the given velocity field if
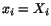 at time
at time 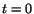 ,
,
- c)
- the principal stretches and the deformed position of the axis
of the maximum principal stretch for the material particle which at
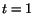 is at
is at 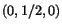 ,
,
- d)
- principal stretchings and their axes for the material particle
which currently is at
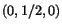 .
.
![]() emanating from a material point located at
emanating from a material point located at
![]() in the
present configuration at time
in the
present configuration at time ![]() . We wish to compute
. We wish to compute
![]() , the rate of
change of length and direction of
, the rate of
change of length and direction of
![]() . Let
. Let
![]() be the deformed position of the material point located at
be the deformed position of the material point located at
![]() in the reference configuration and
in the reference configuration and ![]() that of
that of
![]() . Then
. Then
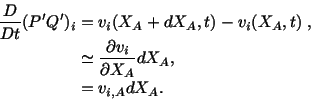
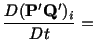
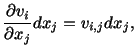
![]() . Let
. Let
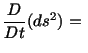
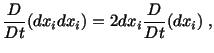
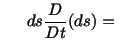
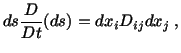
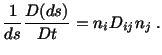
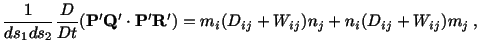
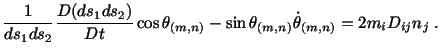
![]() is symmetric, we also have the result that there always exist
three mutually perpendicular directions (eigenvectors of
is symmetric, we also have the result that there always exist
three mutually perpendicular directions (eigenvectors of ![]() ) along which
the stretching (an eigenvalue of
) along which
the stretching (an eigenvalue of ![]() ) is either maximum or minimum
among stretchings for
all differential elements extending from the material particle which
currently is at
) is either maximum or minimum
among stretchings for
all differential elements extending from the material particle which
currently is at ![]() .
.
![]() be a unit eigenvector of
be a unit eigenvector of
![]() , i.e.,
, i.e.,
![]() where
where ![]() is the eigenvalue
corresponding to
is the eigenvalue
corresponding to
![]() . From (3.12.3), we have
. From (3.12.3), we have
![]() does not equal the
rate of change of the rotation matrix
does not equal the
rate of change of the rotation matrix
![]() . Equations (3.12.9) and
(3.13.1)
. Equations (3.12.9) and
(3.13.1)![]() give
give
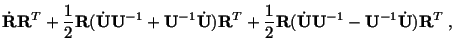
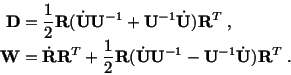
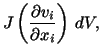
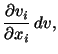
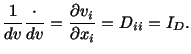
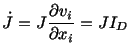
![]() and
taking the time derivative of both sides, we obtain
and
taking the time derivative of both sides, we obtain
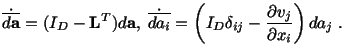
![$\displaystyle [v_{i,j}] = \left[\begin{array}{ccc} 0 & 2 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right]\ .$](img941.gif)
![$\displaystyle 1/2[v_{i,j} + v_{j,i}] = \left[\begin{array}{ccc} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\end{array}\right],$](img942.gif)
![$\displaystyle 1/2[v_{i,j} - v_{j,i}] = \left[\begin{array}{rcc} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0\end{array}\right].$](img943.gif)
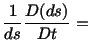
![$\displaystyle (1/\sqrt 5\ \ 2/\sqrt 5\ \ 0)\left[\begin{array}{ccc}0 & 1 & 0\\ ...
...ght]\left[\begin{array}{c} 1/\sqrt 5\\ 2/\sqrt 5\\ 0\end{array}\right] = 4/5\ .$](img948.gif)