The polar decomposition theorem of Cauchy3 states that a non-singular
matrix equals an orthogonal matrix either pre or post multiplied by a positive
definite symmetric matrix. If we apply this theorem to the deformation
gradient
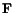 , we get
, we get
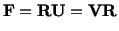 |
(3.13.1) |
in which
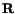 is a proper orthogonal matrix and
is a proper orthogonal matrix and
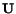 and
and
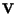 are positive definite symmetric matrices. Note
that the decomposition (3.13.1) of
are positive definite symmetric matrices. Note
that the decomposition (3.13.1) of
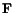 is unique in that
is unique in that
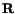 ,
,
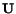 and
and
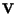 are uniquely determined by
are uniquely determined by
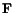 . From (3.13.1) it follows that
. From (3.13.1) it follows that
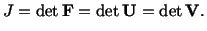 |
(3.13.2) |
Since
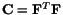 and
and
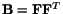 , therefore
, therefore
| |
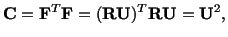 |
(3.13.3) |
| |
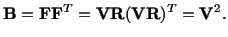 |
(3.13.4) |
We note that
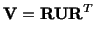 |
(3.13.5) |
and
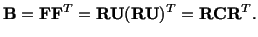 |
(3.13.6) |
Since
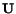 is symmetric, it has at least one orthogonal triad of
eigenvectors. Let
is symmetric, it has at least one orthogonal triad of
eigenvectors. Let
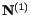 be an eigenvector of
be an eigenvector of
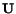 and
and
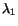 be the corresponding eigenvalue so that
be the corresponding eigenvalue so that
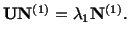 |
(3.13.7) |
Therefore
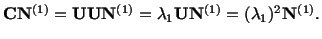 |
(3.13.8) |
Thus
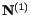 is an eigenvector of
is an eigenvector of
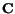 and
the corresponding eigenvalue is
and
the corresponding eigenvalue is
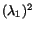 . Since eqn. (3.13.8) holds
for every eigenvector of
. Since eqn. (3.13.8) holds
for every eigenvector of
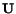 , we conclude that eigenvectors of
, we conclude that eigenvectors of
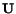 and
and
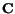 are the same and the eigenvalues of
are the same and the eigenvalues of
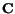 are equal to the squares of the eigenvalues of
are equal to the squares of the eigenvalues of
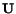 . In section 3.9,
we proved that the eigenvalues of
. In section 3.9,
we proved that the eigenvalues of
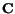 are the squares of the
principal stretches and the eigenvectors of
are the squares of the
principal stretches and the eigenvectors of
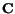 are the axes of
principal stretches also usually called principal axes of stretch
in the reference configuration. Thus eigenvectors of
are the axes of
principal stretches also usually called principal axes of stretch
in the reference configuration. Thus eigenvectors of
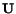 are the principal axes of stretch in the reference
configuration
and the eigenvalues of
are the principal axes of stretch in the reference
configuration
and the eigenvalues of
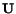 are the princpal stretches. Let us now
find the deformed position of an eigenvector
are the princpal stretches. Let us now
find the deformed position of an eigenvector
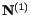 of
of
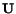 . Since
. Since
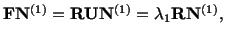 |
(3.13.9) |
therefore
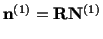 |
(3.13.10) |
points in the direction of the vector into which
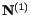 is deformed. Note that
is deformed. Note that
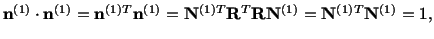 |
(3.13.11) |
therefore,
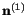 is a unit vector in the direction
of the deformed position of
is a unit vector in the direction
of the deformed position of
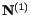 . Now
. Now
 |
(3.13.12) |
Equations (3.13.9), (3.13.10) and (3.13.12) when combined together give
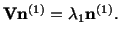 |
(3.13.13) |
Thus 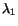 is an eigenvalue of
is an eigenvalue of
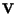 with
with
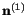 as the eigenvector. This exercise proves that the
eigenvalues of
as the eigenvector. This exercise proves that the
eigenvalues of
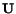 and
and
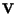 are equal and that the
eigenvectors of
are equal and that the
eigenvectors of
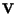 are the deformed positions of the eigenvectors of
are the deformed positions of the eigenvectors of
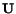 . Thus eigenvectors of
. Thus eigenvectors of
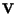 are the deformed position of
the principal axes of stretch. Said differently, eigenvectors of
are the deformed position of
the principal axes of stretch. Said differently, eigenvectors of
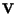 are the principal axes of stretch in the deformed configuration or in
the present configuration. Of course,
are the principal axes of stretch in the deformed configuration or in
the present configuration. Of course,
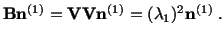 |
(3.13.14) |
From (3.13.14), (3.13.8), (3.13.9) and (3.13.10), we
conclude that eigenvalues of
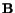 and
and
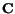 are equal, and the
eigenvectors of
are equal, and the
eigenvectors of
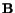 are the principal axes of stretch in the deformed
configuration.
are the principal axes of stretch in the deformed
configuration.
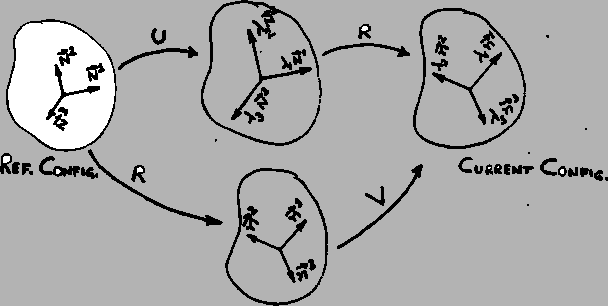
Corresponding to the two decompositions of
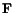 given by (3.13.1) we
can view the deformation of the triad
given by (3.13.1) we
can view the deformation of the triad
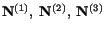 , the eigenvectors of
, the eigenvectors of
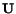 , as a stretch of these axes
followed by a rotation or a rotation of these axes followed by their stretch.
This is schematically shown in the Fig. below.
, as a stretch of these axes
followed by a rotation or a rotation of these axes followed by their stretch.
This is schematically shown in the Fig. below.
Example: For simple shear
- a)
- find the principal stretches,
- b)
- show that the angle
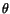 through which the principal axes of stretch in the reference configuration are
rotated so as to become the principal axes of stretch in the present
configuration is given by
through which the principal axes of stretch in the reference configuration are
rotated so as to become the principal axes of stretch in the present
configuration is given by
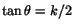 .
.
Solution: For the given deformation
The squares of the principal stretches
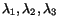 are roots of the equation
are roots of the equation
![$ \det([\mathbf{C}] -
\lambda[\mathbf{1}])=0$](img997.gif)
Note that the given deformation is a plane strain deformation. By
looking at the matrices
![$ [\mathbf{C}]$](img604.gif) and
and
![$ [\mathbf{B}]$](img1004.gif) we see that
we see that
 -axis and
-axis and 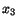 -axis are eigenvectors of
-axis are eigenvectors of
![$ [\mathbf{C}]$](img604.gif) and
and
![$ [\mathbf{B}]$](img1004.gif) corresponding to the eigenvalue one. Also,
corresponding to the eigenvalue one. Also, 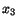 -axis
coincides with the
-axis
coincides with the 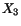 -axis for the given deformation. Thus the rotation of
principal axes of stretch takes place about the
-axis for the given deformation. Thus the rotation of
principal axes of stretch takes place about the 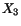 -axis. Let this angle of
rotation be
-axis. Let this angle of
rotation be 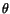 in the clockwise direction. Then
in the clockwise direction. Then
Substituting for
![$ [\mathbf{B}]$](img1004.gif) ,
,
![$ [\mathbf{C}]$](img604.gif) and
and
![$ [\mathbf{R}]$](img1006.gif) in eqn. (3.13.6) we arrive at
in eqn. (3.13.6) we arrive at
Therefore
which gives
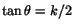 .
.
![]() , we get
, we get
![]() is symmetric, it has at least one orthogonal triad of
eigenvectors. Let
is symmetric, it has at least one orthogonal triad of
eigenvectors. Let
![]() be an eigenvector of
be an eigenvector of
![]() and
and
![]() be the corresponding eigenvalue so that
be the corresponding eigenvalue so that
![]() given by (3.13.1) we
can view the deformation of the triad
given by (3.13.1) we
can view the deformation of the triad
![]() , the eigenvectors of
, the eigenvectors of
![]() , as a stretch of these axes
followed by a rotation or a rotation of these axes followed by their stretch.
This is schematically shown in the Fig. below.
, as a stretch of these axes
followed by a rotation or a rotation of these axes followed by their stretch.
This is schematically shown in the Fig. below.
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ k & 1 & 0\\ 0 & 0 & 1\end{array}\right]\,$](img992.gif)
![$\displaystyle \left[\begin{array}{ccc}1 + k^2 & k & 0\\ k & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\ ,$](img994.gif)
![$\displaystyle \left[\begin{array}{ccc} 1 & k & 0\\ k & 1+k^2 & 0\\ 0 & 0 & 1\end{array}\right]\ .$](img996.gif)
![$\displaystyle [\mathbf{R}] = \left[\begin{array}{ccc}\cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1\end{array}\right]$](img1005.gif)
![$\displaystyle \left[\begin{array}{ccc} 1 & k & 0\\ k & 1+k^2 & 0\\ 0 & 0 & 1\...
...1 + k^2\sin^2\theta + 2k\sin\theta\cos\theta & 0\\ 0 & 0 & 1\end{array}\right]$](img1007.gif)