... magnitude¹

The magnitude of 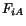$F_{iA}$ is defined as 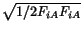$\sqrt{1/2 F_{iA}F_{iA}}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

....²

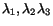$\lambda_1,\lambda_2\lambda_3$ should not be confused with the components of a vector.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Cauchy³

This theorem is proved in any book on linear algebra, e.g. on pg. 83 of P.R. Halmos, Finite Dimensional Vector Spaces, 2nd ed. Van Nostrand, Princeton, Toronto, and London, 1958.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... field.⁴

This requirement is in addition to the condition that 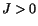$J > 0$ for the given strain field.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.