When the displacements and displacement gradients are small, we can neglect
second order terms in (3.8.6) and approximate the strain tensor by
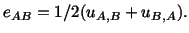 |
(3.14.1) |
Since
where we have neglected the second order term in the displacement
gradients; for infinitesimal deformations,
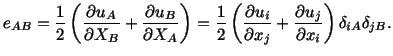 |
(3.14.3) |
Thus one can differentiate displacements with respect to the
current coordinates or the referential coordinates to evaluate the
infinitesimal strain tensor.
Since 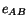 is symmetric, therefore, it has at least one orthogonal triad
of eigenvectors. The eigenvectors of
is symmetric, therefore, it has at least one orthogonal triad
of eigenvectors. The eigenvectors of 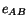 are the principal axes of
engineering strain and its eigenvalues are principal infinitesimal strains.
From equations (3.8.3) and (3.8.6) we obtain
are the principal axes of
engineering strain and its eigenvalues are principal infinitesimal strains.
From equations (3.8.3) and (3.8.6) we obtain
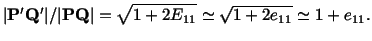 |
(3.14.4) |
Recalling that
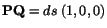 we see that
we see that
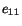 equals the change in length per unit length of an infinitesimal line
element parallel to
equals the change in length per unit length of an infinitesimal line
element parallel to  -axis. Similar interpretation holds for
-axis. Similar interpretation holds for 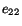 and
and
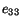 . From equations (3.8.4) and (3.8.6) we conclude that
. From equations (3.8.4) and (3.8.6) we conclude that
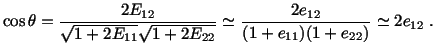 |
(3.14.5) |
Here 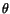 is the angle between the deformed positions of
lines initially parallel to
is the angle between the deformed positions of
lines initially parallel to 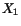 and
and 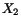 axes. If the change
axes. If the change 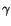 in
the angle is small so that
in
the angle is small so that
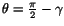 , then
eqn. (3.14.5) becomes
, then
eqn. (3.14.5) becomes
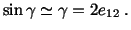 |
(3.14.6) |
Thus 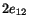 equals the infinitesimal change in the
angle between
two lines originally parallel to
equals the infinitesimal change in the
angle between
two lines originally parallel to 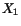 and
and 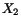 axes. This change in the
angle is called the shearing strain.
axes. This change in the
angle is called the shearing strain.
From equations (3.9.3) and (3.8.6) we obtain
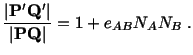 |
(3.14.7) |
Thus the engineering strain in any direction
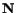 equals
equals
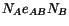 . One can similarly show that the shearing strain
between two orthogonal directions
. One can similarly show that the shearing strain
between two orthogonal directions
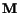 and
and
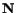 equals
equals
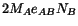 . Recalling that
. Recalling that
and that
we obtain
![$\displaystyle [\mathbf{C}]=\ $](img993.gif) |
![$\displaystyle [\mathbf{F}]^T[\mathbf{F}]\simeq [\mathbf{1}] + [\mathbf{H}] + [\mathbf{H}]^T\ ,$](img1032.gif) |
(3.14.8) |
![$\displaystyle [\mathbf{U}] =\ $](img1033.gif) |
![$\displaystyle [\mathbf{C}]^{1/2} \simeq [\mathbf{1}] + \frac{1}{2}([\mathbf{H}] + [\mathbf{H}]^T)\ ,$](img1034.gif) |
|
 |
![$\displaystyle [\mathbf{1}] + [\mathbf{e}]\ ,$](img1035.gif) |
(3.14.9) |
![$\displaystyle [\mathbf{R}] =\ $](img1036.gif) |
![$\displaystyle [\mathbf{F}][\mathbf{U}]^{-1}$](img1037.gif) |
|
 |
![$\displaystyle ([\mathbf{1}] + [\mathbf{H}])([\mathbf{1}] + [\mathbf{e}])^{-1}$](img1038.gif) |
|
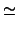 |
![$\displaystyle [\mathbf{1}] + \frac{1}{2}([\mathbf{H}] - [\mathbf{H}]^T)\ .$](img1039.gif) |
(3.14.10) |
The skew symmetric tensor
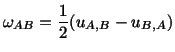 |
(3.14.11) |
gives the infinitesimal rotation. For any infinitesimal vector
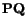 we have
we have
and therefore
![$\displaystyle \{\mathbf{P}^\prime \mathbf{Q}^\prime\} - \{\mathbf{PQ}\} = [\mathbf{e}]\{\mathbf{PQ}\} + [{\mbox{\boldmath {$\omega$}}}]\{\mathbf{PQ}\}\ .$](img1043.gif) |
(3.14.12) |
Thus the deformation of a line element
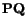 equals the sum of the deformations caused by the infinitesimal strain tensor
and the infinitesimal rotation tensor. Similarly, if
equals the sum of the deformations caused by the infinitesimal strain tensor
and the infinitesimal rotation tensor. Similarly, if
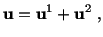 |
(3.14.13) |
then
| |
![$\displaystyle [\mathbf{e}] = [\mathbf{e}^1] + [\mathbf{e}^2]\ ,$](img1045.gif) |
(3.14.14) |
| |
![$\displaystyle [{\mbox{\boldmath {$\omega$}}} ] = [{\mbox{\boldmath {$\omega$}}}^1] + [{\mbox{\boldmath {$\omega$}}}^2]\ .$](img1046.gif) |
(3.14.15) |
Thus the infinitesimal strains and rotations caused by a given
displacement equal the sum of the infinitesimal strains and rotations caused
by the components of the given displacement.
Exercise: Prove that for small deformations
| |
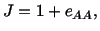 |
(3.14.16) |
| |
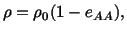 |
(3.14.17) |
and for isochoric deformations
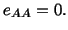 |
(3.14.18) |
Exercise: Consider the displacement field
Using both the infinitesimal strain theory and the finite
strain theory, find the change in length per unit length for the material line
element
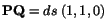 that emanates from the material
particle
that emanates from the material
particle
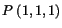 in the reference configuration for
in the reference configuration for
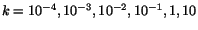 . Plot these changes as a function of
. Plot these changes as a function of
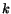 .
.
Exercise: With reference to a rectangular Cartesian
coordinate system, the state of strain at a point is given by the matrix.
- a)
- What is the engineering strain in the direction
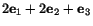 at the point
at the point
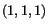 in the reference configuration?
in the reference configuration?
- b)
- What is the shearing strain between two perpendicular lines (in the
reference configuration) emanating from the point
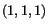 in the directions
of
in the directions
of
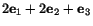 and
and
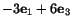 ?
?
For an infinitesimal rigid body motion, the displacement vector
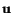 is given by
is given by
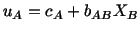 |
(3.14.19) |
in which 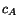 is a constant and
is a constant and
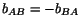 is a
skew-symmetric tensor. For the displacement given by (3.14.19),
is a
skew-symmetric tensor. For the displacement given by (3.14.19),
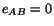 .
Naturally the following question arises: Is the rigid body motion the only
deformation for which the infinitesimal strain tensor vanishes identically?
The answer, as proved in the following example, is yes.
.
Naturally the following question arises: Is the rigid body motion the only
deformation for which the infinitesimal strain tensor vanishes identically?
The answer, as proved in the following example, is yes.
Example: Regarding
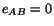 as six partial differential
equations, solve for
as six partial differential
equations, solve for
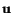 .
.
Solution:
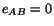 corresponds to
corresponds to
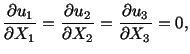 |
(3.14.20) |
and
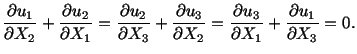 |
(3.14.21) |
By differentiating (3.14.21)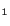 with respect to
with respect to 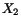 and
(3.14.21)
and
(3.14.21)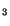 with respect to
with respect to 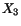 and making use of (3.14.20)
and making use of (3.14.20)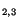 we
obtain
we
obtain
This when combined with (3.14.20)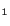 yields
yields
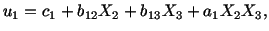 |
(3.14.22) |
in which
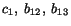 and
and 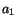 are constants. By
following a procedure similar to that used to obtain (3.14.22) for
are constants. By
following a procedure similar to that used to obtain (3.14.22) for 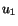 , we
obtain for
, we
obtain for 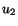 and
and 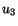 the following.
the following.
| |
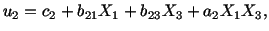 |
(3.14.23) |
| |
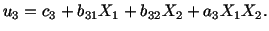 |
(3.14.24) |
Substituting from (3.14.22), (3.14.23) and (3.14.24) into (3.14.21) we get
Since these equations hold for all values of
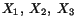 which correspond to various points in the body, therefore,
which correspond to various points in the body, therefore,
The last set of equations implies that
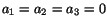 . From
the other set of equations, it follows that
. From
the other set of equations, it follows that
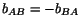 . Hence
equations (3.14.22), (3.14.23) and (3.14.24) which are a solution of
. Hence
equations (3.14.22), (3.14.23) and (3.14.24) which are a solution of
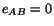 reduce to
reduce to
Recalling equations (3.14.13) and (3.14.14) we see that the strain caused by
displacements
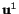 and
and
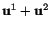 is the same if
is the same if
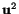 is a rigid body motion.
To prevent the rigid motion of a body, one needs to fix three noncolinear
points of the body.
is a rigid body motion.
To prevent the rigid motion of a body, one needs to fix three noncolinear
points of the body.
The strain field given by eqns. (3.14.20) and (3.14.21) is a very special
one in that it is identically zero throughout the body. What if we were given
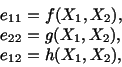 |
(3.14.25) |
and asked to find the corresponding two-dimensional displacement
field? Can we always find a displacement field that will produce the strains
specified by (3.14.25)? The answer is of course no. Since
therefore,
If we substitute for
 and
and 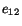 from (3.14.25) we obtain
from (3.14.25) we obtain
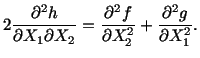 |
(3.14.26) |
Thus unless the given functions 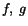 , and
, and 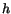 satisfy
(3.14.26) we will not be able to find a displacement field that will produce
the desired strain field.4 Another way of saying
essentially the same thing is that we have three
equations (3.14.25)
satisfy
(3.14.26) we will not be able to find a displacement field that will produce
the desired strain field.4 Another way of saying
essentially the same thing is that we have three
equations (3.14.25)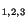 for
two unknowns
for
two unknowns 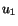 and
and 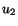 . Unless the given expressions for
. Unless the given expressions for 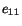 ,
,
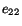 and
and 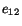 are related somehow, we will not, in general, be able to
find
are related somehow, we will not, in general, be able to
find 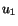 and
and 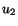 . That relation is the equation (3.14.26) which is
known as
a compatability condition. In the three dimensional case we can derive
compatability conditions like (3.14.26) in a similar way. However, another,
perhaps neater, approach to the problem is the following.
. That relation is the equation (3.14.26) which is
known as
a compatability condition. In the three dimensional case we can derive
compatability conditions like (3.14.26) in a similar way. However, another,
perhaps neater, approach to the problem is the following.
Given the displacement
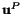 of a point
of a point  in the body and the
strain field
in the body and the
strain field 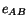 in the neighborhood of
in the neighborhood of  , we would like to find the
displacement
, we would like to find the
displacement
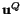 of a neighboring point
of a neighboring point 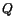 . Now
. Now
Note that
where we have integrated by parts. Combining (3.14.27) and
(3.14.28) we obtain
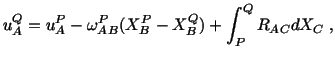 |
(3.14.29) |
where
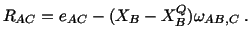 |
(3.14.30) |
Since the path of integration in (3.14.29) from point  to
point
to
point  is arbitrary, in order to obtain a unique value of
is arbitrary, in order to obtain a unique value of
 ,
the integral in eqn. (3.14.29) must be path independent. The necessary and
sufficient condition for this is
,
the integral in eqn. (3.14.29) must be path independent. The necessary and
sufficient condition for this is
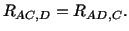 |
(3.14.31) |
Substituting from (3.14.30) into (3.14.31) and noting that
we arrive at
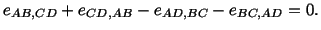 |
(3.14.32) |
Even though there are 81 equations given by (3.14.32) only the
following six are non-trivial.
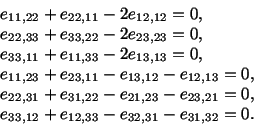 |
(3.14.33) |
Out of these six equations only three are linearly independent.
However, we will not prove that here.
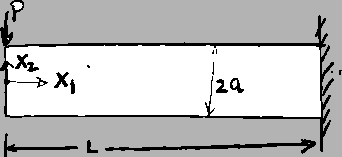
Example: For the two-dimensional small strain theory,
the strains for a cantilever beam are given by
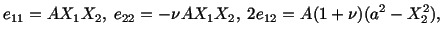 |
(3.14.31) |
where 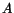 ,
, 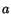 ,
, 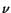 are positive constants and
are positive constants and
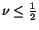 . Assume that the displacements
. Assume that the displacements 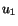 ,
, 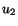 relative to axes
relative to axes
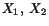 are functions of
are functions of 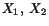 .
.
- a)
- Show that continuous single-valued displacements
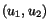 are possible.
are possible.
- b)
- Hence derive formulas for
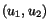 as explicit functions of
as explicit functions of
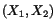 with the conditions
with the conditions
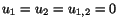 for
for
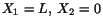 .
.
Solution: a) From the given expressions for
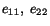 and
and 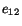 we obtain
we obtain
so that the only non-trivial compatability equation (3.14.33)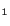 is
satisfied.
is
satisfied.
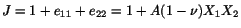 . For the given
constraints on
. For the given
constraints on
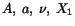 and
and 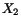 ,
,
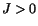 . Thus continuous single-valued displacements are possible.
. Thus continuous single-valued displacements are possible.
b) Integrating
we obtain
Substituting for 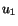 and
and 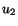 into
into
we obtain
Since the left-hand side of this equation is a function of
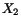 and the right-hand side a function of
and the right-hand side a function of 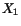 , for the two sides to be
always equal, each must equal a constant say
, for the two sides to be
always equal, each must equal a constant say 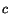 . Thus
. Thus
Therefore
where 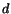 and
and 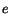 are constants of integration. Thus
are constants of integration. Thus
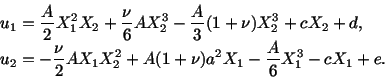 |
(3.14.32) |
In order that
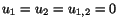 for
for
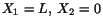 we must have
we must have
Substituting for 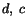 and
and 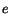 into (3.14.32) we arrive at the following.
into (3.14.32) we arrive at the following.
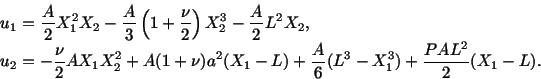 |
(3.14.34) |
For points on the plane 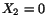 ,
,
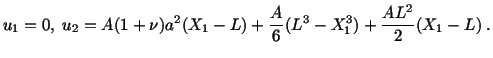 |
(3.14.33) |
Thus longitudinal lines on the plane 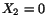 which is the
neutral surface are not stretched. However, points on the longitudinal line
do move vertically. Equation (3.14.34) corresponds to the deflection
equation usually studied in the first Strength of Materials or Mechanics of
Deforms course.
However, in that course the following boundary conditions are used. For
which is the
neutral surface are not stretched. However, points on the longitudinal line
do move vertically. Equation (3.14.34) corresponds to the deflection
equation usually studied in the first Strength of Materials or Mechanics of
Deforms course.
However, in that course the following boundary conditions are used. For
With these, eqn. (3.14.32) gives
Thus
which agrees with the strength of materials solution.
Exercise: Check whether or not the following distribution
of the state of infinitesimal strain satisfies the compatability conditions:
Exercise: Given the strain field
and all other
 ,
,
- a)
- Does it satisfy the equations of compatability?
- b)
- By attempting to integrate the strain field, show that it cannot
correspond to a displacement field.
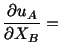
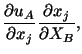
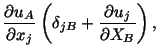
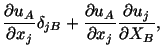
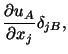
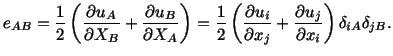
![]() is symmetric, therefore, it has at least one orthogonal triad
of eigenvectors. The eigenvectors of
is symmetric, therefore, it has at least one orthogonal triad
of eigenvectors. The eigenvectors of ![]() are the principal axes of
engineering strain and its eigenvalues are principal infinitesimal strains.
From equations (3.8.3) and (3.8.6) we obtain
are the principal axes of
engineering strain and its eigenvalues are principal infinitesimal strains.
From equations (3.8.3) and (3.8.6) we obtain
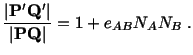
![$\displaystyle [\mathbf{C}]^{1/2} \simeq [\mathbf{1}] + \frac{1}{2}([\mathbf{H}] + [\mathbf{H}]^T)\ ,$](img1034.gif)
![$\displaystyle [\mathbf{1}] + \frac{1}{2}([\mathbf{H}] - [\mathbf{H}]^T)\ .$](img1039.gif)
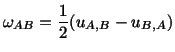
![$\displaystyle [\mathbf{e}] = 10^{-4}\left[\begin{array}{crr} 5 & 3 & 0\\ 3 & 4 & -1\\ 0 & -1 & 2\end{array}\right].$](img1053.gif)
![]() is given by
is given by
![]() as six partial differential
equations, solve for
as six partial differential
equations, solve for
![]() .
.
![]() corresponds to
corresponds to
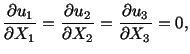
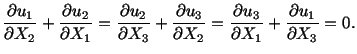
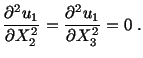
![]() and
and
![]() is the same if
is the same if
![]() is a rigid body motion.
To prevent the rigid motion of a body, one needs to fix three noncolinear
points of the body.
is a rigid body motion.
To prevent the rigid motion of a body, one needs to fix three noncolinear
points of the body.
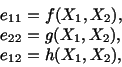
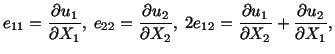
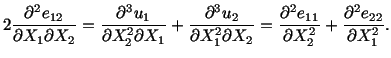
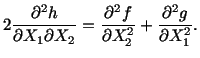
![]() of a point
of a point ![]() in the body and the
strain field
in the body and the
strain field ![]() in the neighborhood of
in the neighborhood of ![]() , we would like to find the
displacement
, we would like to find the
displacement
![]() of a neighboring point
of a neighboring point ![]() . Now
. Now
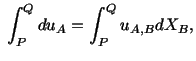
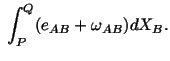
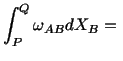
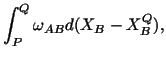
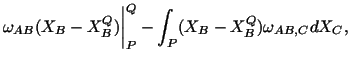
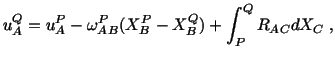
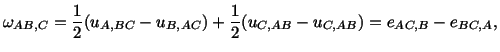
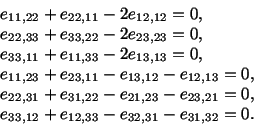
![]() and
and ![]() we obtain
we obtain
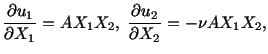
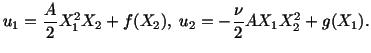
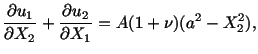
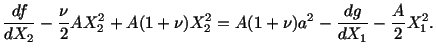
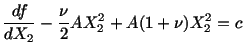
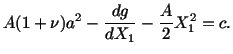
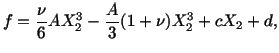
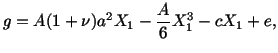
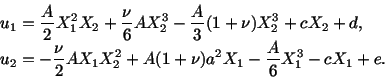
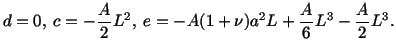
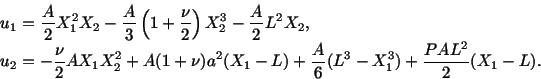
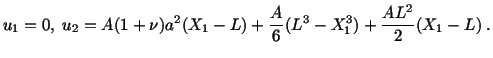
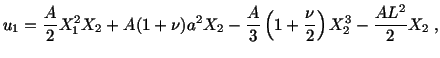
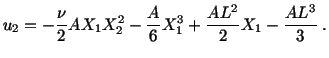
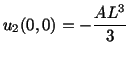
![$\displaystyle [\mathbf{e}] = \left[\begin{array}{ccc} X^2_1 & X^2_2 + X^2_3 & X_1X_3\\ X^2_2 + X^2_3 & 0 & X_1\\ X_1X_3 & X_1 & X^2_2\end{array}\right].$](img1140.gif)