
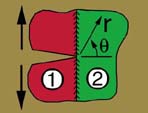
Figure 2. Schematic of Mode-I cracks spanning the length scales
Ronald D. Kriz, Associate Professor
Engineering Science and Mechanics
Virginia Polytechnic Institute and State University
Blacksburg, Virginia 24061
Cracks span the scales. The mechanical behavior of materials with cracks can be modeled to include: 1) the influence of individual atoms ("nano"), 2) the presence of interfacial layers separating different microstructures ("micro"), or 3) the idealized continuum model where atomic and interfacial effects are neglected ("macro"). Regardless of the scale, models make simplifying approximations. Understanding these approximations is key to understanding how some models bridge the scales. Therefore we will highlight these approximations below as we develope the theory and also when we develope the mathematical model for each of the scales. The images on the home page exemplify these three scales.



In this section we focus our attention on modeling the mechanical behavior of materials that are influenced by cracks at or near interfacial layers or grain boundaries. The image in the center of Fig. 2 shows a schematic of a crack that has intersected a boundary between two dissimilar materials: region 1 and region 2. This boundary can be a grain boundary or interfacial layer separating two different lamina in a composite laminate. In either case the model for predicting the behavior of crack propagation is fundamentally the same but in the following sections we will focus mostly on interfaces in laminated composites.